Analysis of Underactuated Dynamic Locomotion Systems Using Perturbation Expansion: The Twistcar Toy Example | Journal of Nonlinear Science Skip to main content
Springer Nature Link
Log in

Analysis of Underactuated Dynamic Locomotion Systems Using Perturbation Expansion: The Twistcar Toy Example

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

Abstract

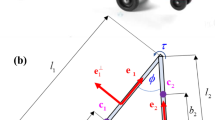
Underactuated robotic locomotion systems are commonly represented by nonholonomic constraints where in mixed systems, these constraints are also combined with momentum evolution equations. Such systems have been analyzed in the literature by exploiting symmetries and utilizing advanced geometric methods. These works typically assume that the shape variables are directly controlled, and obtain the system’s solutions only via numerical integration. In this work, we demonstrate utilization of the perturbation expansion method for analyzing a model example of mixed locomotion system—the twistcar toy vehicle, which is a variant of the well-studied roller-racer model. The system is investigated by assuming small-amplitude oscillatory inputs of either steering angle (kinematic) or steering torque (mechanical), and explicit expansions for the system’s solutions under both types of actuation are obtained. These expressions enable analyzing the dependence of the system’s dynamic behavior on the vehicle’s structural parameters and actuation type. In particular, we study the reversal in direction of motion under steering angle oscillations about the unfolded configuration, as well as influence of the choice of actuation type on convergence properties of the motion. Some of the findings are demonstrated qualitatively by reporting preliminary motion experiments with a modular robotic prototype of the vehicle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Bloch, A.M.: Nonholonomic Mechanics and Control, vol. 24. Springer, Berlin (2003)

    Google Scholar 

  • Bloch, A.M., Marsden, J.E., Zenkov, D.V.: Nonholonomic dynamics. Not. AMS 52(3), 320–329 (2005)

    MathSciNet  MATH  Google Scholar 

  • Bullo, F., Žefran, M.: On mechanical control systems with nonholonomic constraints and symmetries. Syst. Control Lett. 45(2), 133–143 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  • Chakon, O.: Theoretical and experimental investigation of the twistcar vehicle’s dynamics. M.Sc Thesis at Technion, Haifa, Israel (primary language: Hebrew) (2015)

  • Chitta, S., Cheng, P., Frazzoli, E., Kumar, V.: Robotrikke: a novel undulatory locomotion system. In: Proceedings of the 2005 IEEE International Conference on Robotics and Automation, 2005. ICRA 2005, pp. 1597–1602 (2005)

  • Chitta, S., Kumar, V.: Dynamics and generation of gaits for a planar rollerblader. In: Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2003. (IROS 2003), vol. 1, pp. 860–865 (2003)

  • Dear, T., Kelly, S.D., Travers, M., Choset, H.: Mechanics and control of a terrestrial vehicle exploiting a nonholonomic constraint for Fishlike locomotion. In: ASME 2013 Dynamic Systems and Control Conference, pp. V002T33A004–V002T33A004 (2013)

  • Dreyfus, R., Baudry, J., Roper, M.L., Fermigier, M., Stone, H.A., Bibette, J.: Microscopic artificial swimmers. Nature 437(7060), 862–865 (2005)

    Article  MATH  Google Scholar 

  • Fedonyuk, V., Tallapragada, P.: The stick-slip motion of a Chaplygin Sleigh with a piecewise smooth nonholonomic constraint. In: ASME 2015 Dynamic Systems and Control Conference, pp. V003T49A004–V003T49A004 (2015)

  • Gutman, E., Or, Y.: Simple model of a planar undulating magnetic microswimmer. Phys. Rev. E 90(1), 013012 (2014)

    Article  Google Scholar 

  • Gutman, E., Or, Y.: Symmetries and gaits for Purcell’s Three-Link Microswimmer model. IEEE Trans. Robot. 32(1), 53–69 (2016)

    Article  Google Scholar 

  • Hatton, R.L., Choset, H.: Geometric swimming at low and high Reynolds numbers. IEEE Trans. Robot. 29(3), 615–624 (2013)

    Article  Google Scholar 

  • Kanso, E., Marsden, J.E., Rowley, C.W., Melli-Huber, J.B.: Locomotion of articulated bodies in a perfect fluid. J. Nonlinear Sci. 15(4), 255–289 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  • Kelly, S.D., Fairchild, M.J., Hassing, P.M., Tallapragada, P.: Proportional heading control for planar navigation: the Chaplygin beanie and fishlike robotic swimming. In: 2012 American Control Conference (ACC), pp. 4885–4890 (2012)

  • Kelly, S.D., Murray, R.M.: Geometric phases and robotic locomotion. J. Robot. Syst. 12(6), 417–431 (1995)

    Article  MATH  Google Scholar 

  • Krishnaprasad, P.S., Tsakiris, D.P.: Oscillations, SE (2)-snakes and motion control: a study of the roller racer. Dyn. Syst. Int. J. 16(4), 347–397 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • Melli, J.B., Rowley, C.W., Rufat, D.S.: Motion planning for an articulated body in a perfect planar fluid. SIAM J. Appl. Dyn. Syst. 5(4), 650–669 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  • Murray, R.M., Li, Z., Sastry, S.S., Sastry, S.S.: A Mathematical Introduction to Robotic Manipulation. CRC Press, Boca Raton (1994)

    MATH  Google Scholar 

  • Nayfeh, A.H.: Perturbation Methods. Wiley, London (2008)

    Google Scholar 

  • Neimark, J.I., Fufaev, N.A.: Dynamics of Nonholonomic Systems, vol. 33. American Mathematical Society, Providence (2004)

    MATH  Google Scholar 

  • Ostrowski, J., Burdick, J., Lewis, A. D., Murray, R. M.: The mechanics of undulatory locomotion: the mixed kinematic and dynamic case. In: Proceedings., 1995 IEEE International Conference on Robotics and Automation, 1995, vol. 2, pp. 1945–1951 (1995)

  • Ostrowski, J., Lewis, A., Murray, R., Burdick, J: Nonholonomic mechanics and locomotion: the snakeboard example. In: Proceedings., 1994 IEEE International Conference on Robotics and Automation, 1994 (pp. 2391–2397) (1994)

  • Ostrowski, J., Burdick, J.: The geometric mechanics of undulatory robotic locomotion. Int. J. Robot. Res. 17(7), 683–701 (1998)

    Article  Google Scholar 

  • Shammas, E.A., Choset, H., Rizzi, A.A.: Geometric motion planning analysis for two classes of underactuated mechanical systems. Int. J. Robot. Res. 26(10), 1043–1073 (2007)

    Article  Google Scholar 

  • Shapere, A., Wilczek, F.: Geometry of self-propulsion at low Reynolds number. J. Fluid Mech. 198, 557–585 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  • Stanchenko, S.V.: Non-holonomic Chaplygin systems. J. Appl. Math. Mech. 53(1), 11–17 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  • Vela, P.A., Burdick, J.W.: Control of biomimetic locomotion via averaging theory. In: IEEE International Conference on Robotics and Automation, vol. 1, pp. 1482–1489 (2003)

  • Vela, P.A., Burdick, J.W.: Control of underactuated driftless systems using higher-order averaging theory. In: Proceedings of the American Control Conference, vol. 2, pp. 1536–1541 (2003)

  • Vela, P.A., Morgansen, K.A., Burdick, J.W.: Underwater locomotion from oscillatory shape deformations (I). In: IEEE Conference on Decision and Control, vol. 2, pp. 2074–2080 (2002)

  • Wiezel O., Or, Y.: Optimization and small-amplitude analysis of Purcell’s three-link microswimmer model. Proc. R. Soc. A 472, 20160425 (2016). doi:10.1098/rspa.2016.0425

  • Zenkov, D.V., Bloch, A.M., Marsden, J.E.: The energy-momentum method for the stability of non-holonomic systems. Dyn. Stab. Syst. 13(2), 123–165 (1998)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Technion - Israel Institute of Technology, 3200003, Haifa, Israel

    Ofir Chakon & Yizhar Or

Authors
  1. Ofir Chakon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yizhar Or
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yizhar Or.

Additional information

Communicated by Paul Newton.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (mp4 47426 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chakon, O., Or, Y. Analysis of Underactuated Dynamic Locomotion Systems Using Perturbation Expansion: The Twistcar Toy Example. J Nonlinear Sci 27, 1215–1234 (2017). https://doi.org/10.1007/s00332-016-9357-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00332-016-9357-y

Keywords

Mathematics Subject Classification

Search

Navigation