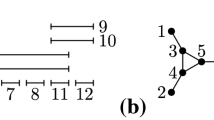
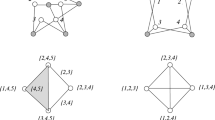
Abstract
A hypergraph is linear if any two distinct hyperedges have at most one common vertex. The existence of a polynomial algorithm is shown for deciding whether a graph of minimum degree δ ≥ 19 is the intersection graph of a linear 3-uniform hypergraph. This result improves a corollary of the finite forbidden subgraph characterization proved for δ ≥ 69 by Naik et al. in [8]. Essentially the same methods yield a polynomial recognition algorithm for the intersection graph of a linear r-uniform hypergraph, r ≥ 3, provided the minimum edge-degree of the graphs is at least 2r 2 − 3r + 1. This improves on the cubic bound that follows from the corresponding finite characterization result in [8].
Similar content being viewed by others
References
Beineke, L.W.: On derived graphs and digraphs. In: H. Saks et al.: Beiträge zur Graphentheorie pp. 17–23 Leipzig: Teubner, 1968
Berge, C., Graphs and Hypergraphs. London: North-Holland 1973
Berge, C., Hypergraphs, Combinatorics of Finite Sets. Amsterdam: North-Holland 1989
Bermond, J.C., Heydemann, M.C., Sotteau, D.: Line graphs of hypergraphs I. Discrete Math. 18, 235–241 (1977)
Heydemann, M.C., Sotteau, D.: Line graphs of hypergraphs II. Colloq. Math. Soc. J. Bolyai 18, 567–582 (1976)
Jacobson, M.S., Kézdy, A.E., Lehel, J.: Intersection graphs associated with uniform hypergraphs, submitted for publication.
Jacobson, M.S., Kézdy, A.E., Lehel, J.: Recognizing triangle-free graphs with induced path-cycle double covers is NP-complete, submitted for publication.
Naik, R.N., Rao, S.B., Shrikhande, S.S., Singhi, N.M.: Intersection graphs of k-uniform linear hypergraphs. Europ. J. Combinatorics 3, 159–172 (1982)
Roussopoulos, N.D.: A max {m, n} algorithm for determining the graph H from its line graph G. Inform. Process. Lett. 2, 108–112 (1973)
van Rooij, A.C.M., Wilf, H.S.: The interchange graph of a finite graph. Acta Math. Acad. Sci. Hungar. 16 263–269 (1965)
Author information
Authors and Affiliations
Additional information
Research supported by ONR Grant Number N00014-91-J-1098
Research supported by OTKA Grant Number 2570
Rights and permissions
About this article
Cite this article
Jacobson, M.S., Kézdy, A.E. & Lehel, J. Recognizing Intersection Graphs of Linear Uniform Hypergraphs. Graphs and Combinatorics 13, 359–367 (1997). https://doi.org/10.1007/BF03353014
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03353014