Abstract
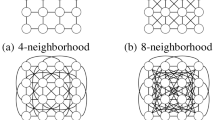
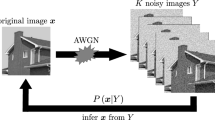
In this paper we compare two iterative approaches to the problem of pixel-level image restoration when the model contains unknown parameters. Pairwise interaction models are assumed to represent the local associations in the true scene. The first approach is a variation on the EM algorithm in which Mean-field approximations are used in the E-step and a variational approximation is used in the M-step. In the second approach, each iteration involves first restoring the image using the Iterated Conditional Modes (ICM) algorithm and then updating the parameter estimates by maximising the so-called pseudolikelihood. In addition, refinemenrs are made to the Mean-field approximation, and these are also used for restoration. The methods are compared empirically using both artificial and real noise-corrupted binary scenes. Within the comparisons the effects of using different convergence criteria for deciding when to stop the algorithms are also investigated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Dempster AP, Laird NM, Rubin DB. Maximum likelihood estimation from incomplete data via the EM algorithm (with discussion). Journal of the Royal Statistical Society, Series B 1977; 39(1): 1–38
Besag J. On the statistical analysis of dirty pictures (with discussion). Journal of the Royal Statistical Society, Series B 1986; 48(3): 259–302
Zhang J. The Mean Field Theory in EM procedures for Markov random fields. IEEE Transactions on Signal Processing 1992; 40(10): 2570–2583
Zhang J. The Mean Field Theory in EM procedures for blind Markov random field image restoration. IEEE Transactions on Image Processing 1993; 2(1): 27–40
Grenander U, Miller MI. Representations of knowledge in complex systems (with discussion). Journal of the Royal Statistical Society, Series B 1994; 56(4): 549–603
Besag J. Spatial interaction and statistical analysis of lattice systems (with discussion). Journal of the Royal Statistical Society, Series B 1974; 36(2): 192–236
Kashyap RL, Chellappa R. Estimation and choice of neighbors in spatial-interaction models of images. IEEE Transactions on Information Theory 1982; 29(1): 60–72
McLachlan GJ, Krishnan T. The EM Algorithm and its Extensions. Wiley, New York, 1997
Dunmur AP, Titterington DM. On a modification to the meanfield EM algorithm in factorial learning. In: Mozer MC, Jordan MI, Petsche T (eds). Advances in Neural Information Processing Systems, Vol. 9, MIT Press, 1997, pp. 431–437
Besag J. Statistical analysis of non-lattice data. The Statistician 1975; 24: 179–195
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Dunmur, A.P., Titterington, D.M. Mean fields and two-dimensional Markov random fields in image analysis. Pattern Analysis & Applic 1, 248–260 (1998). https://doi.org/10.1007/BF01234771
Received:
Revised:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01234771