Abstract
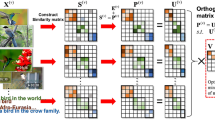
Multi-view clustering is an unsupervised learning strategy that divides data into multiple categories based on complementary and consistent information. Graph-based multi-view clustering methods have attracted much attention due to their simplicity and efficiency. Although graph-based multi-view clustering algorithms have achieved good clustering performance, there are still some issues that need to be addressed. Firstly, existing methods fail to consider the manifold topological structure in the data, which might cause that the constructed similarity graphs are low-quality. Secondly, many graph-based multi-view clustering algorithms treat the construction of similarity graphs and the learning of consistent spectral embedding as two separate procedures, in which the quality of similarity graphs heavily affects the clustering performance. To overcome these problems, we propose a novel method termed as Multi-view Spectral Clustering based on Topological Manifold Learning (MSCTML), where both similarity graph construction and consistent spectral embedding learning are jointly performed in an unified framework. Concretely, affine graph is initially constructed for each view. Subsequently, considering the manifold topological structure in the data, similarity graphs for different views are generated by using the above affine graphs. Furthermore, consistent spectral embedding is learned based on the constructed similarity graphs. Finally, the clustering result is obtained by K-means algorithm. The proposed method is tested on six benchmark datasets. Comparing with single-view and state-of-the-art multi-view clustering algorithms, extensive experimental results demonstrate the superior clustering performance of the proposed MSCTML method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Zhang, L., Shi, Z., Cheng, M.M., Liu, Y., Bian, J.W., Zhou, J.T., Zeng, Z.: Nonlinear regression via deep negative correlation learning. IEEE Trans. Pattern Anal. Mach. Intell. 43(3), 982–998 (2019)
Kanaan-Izquierdo, S., Ziyatdinov, A., Perera-Lluna, A.: Multiview and multifeature spectral clustering using common eigenvectors. Pattern Recogn. Lett. 102, 30–36 (2018)
Ahuja, R., Chug, A., Gupta, S., Ahuja, P., Kohli, S.: Classification and clustering algorithms of machine learning with their applications. In: Nature-Inspired Computation in Data Mining and Machine Learning, pp. 225–248 (2020)
Gao, H., Nie, F., Li, X., Huang, H.: Multi-view subspace clustering. In: IEEE International Conference on Computer Vision, pp. 4238–4246 (2015)
Cao, X., Zhang, C., Fu, H., Liu, S., Zhang, H.: Diversity-induced multi-view subspace clustering. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 586–594 (2015)
Dornaika, F., El Hajjar, S.: Single phase multi-view clustering using unified graph learning and spectral representation. Inf. Sci. 645, 119366 (2023)
Zhao, M., Yang, W., Nie, F.: Deep multi-view spectral clustering via ensemble. Pattern Recogn. 144, 109836 (2023)
Zhao, H., Ding, Z., Fu, Y.: Multi-view clustering via deep matrix factorization. In: AAAI Conference on Artificial Intelligence, vol. 31 (2017)
Huang, S., Kang, Z., Xu, Z.: Auto-weighted multi-view clustering via deep matrix decomposition. Pattern Recogn. 97, 107015 (2020)
Li, Z., Tang, C., Liu, X., Zheng, X., Zhang, W., Zhu, E.: Consensus graph learning for multi-view clustering. IEEE Trans. Multimedia 24, 2461–2472 (2021)
Wen, J., Yan, K., Zhang, Z., Xu, Y., Wang, J., Fei, L., Zhang, B.: Adaptive graph completion based incomplete multi-view clustering. IEEE Trans. Multimedia 23, 2493–2504 (2020)
Zhang, X., Ren, Z., Sun, H., Bai, K., Feng, X., Liu, Z.: Multiple kernel low-rank representation-based robust multi-view subspace clustering. Inf. Sci. 551, 324–340 (2021)
Zheng, Y., Zhang, X., Xu, Y., Qin, M., Ren, Z., Xue, X.: Robust multi-view subspace clustering via weighted multi-kernel learning and co-regularization. IEEE Access 8, 113030–113041 (2020)
Qin, Y., Wu, H., Zhang, X., Feng, G.: Semi-supervised structured subspace learning for multi-view clustering. IEEE Trans. Image Process. 31, 1–14 (2021)
Zhao, N., Bu, J.: Robust multi-view subspace clustering based on consensus representation and orthogonal diversity. Neural Netw. 150, 102–111 (2022)
Ng, A., Jordan, M., Weiss, Y.: On spectral clustering: analysis and an algorithm. Adv. Neural Inf. Process. Syst. 14 (2001)
Yang, Y., Xu, D., Nie, F., Yan, S., Zhuang, Y.: Image clustering using local discriminant models and global integration. IEEE Trans. Image Process. 19(10), 2761–2773 (2010)
Zhao, Z., Wang, L., Liu, H., Ye, J.: On similarity preserving feature selection. IEEE Trans. Knowl. Data Eng. 25(3), 619–632 (2011)
Nie, F., Wang, X., Huang, H.: Clustering and projected clustering with adaptive neighbors. In: 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 977–986 (2014)
Gao, H., Nie, F., Li, X., Huang, H.: Multi-view subspace clustering. In: IEEE International Conference on Computer Vision, pp. 4238–4246 (2015)
Cao, X., Zhang, C., Fu, H., Liu, S., Zhang, H.: Diversity-induced multi-view subspace clustering. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 586–594 (2015)
Wang, X., Guo, X., Lei, Z., Zhang, C., Li, S.Z.: Exclusivity-consistency regularized multi-view subspace clustering. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 923–931 (2017)
Nie, F., Cai, G., Li, X.: Multi-view clustering and semi-supervised classification with adaptive neighbours. In: AAAI Conference on Artificial Intelligence, vol. 31 (2017)
Li, Z., Tang, C., Liu, X., Zheng, X., Zhang, W., Zhu, E.: Consensus graph learning for multi-view clustering. IEEE Trans. Multimedia 24, 2461–2472 (2021)
Zhang, Z., Wang, J., Zha, H.: Adaptive manifold learning. IEEE Trans. Pattern Anal. Mach. Intell. 34(2), 253–265 (2011)
Minh, H.Q., Bazzani, L., Murino, V.: A unifying framework in vector-valued reproducing kernel hilbert spaces for manifold regularization and co-regularized multi-view learning. J. Mach. Learn. Res. 17(25), 1–72 (2016)
Wang, Q., Chen, M., Li, X.: Quantifying and detecting collective motion by manifold learning. In: AAAI Conference on Artificial Intelligence, vol. 31 (2017)
Huang, S., Wu, H., Ren, Y., Tsang, I., Xu, Z., Feng, W., Lv, J.: Multi-view subspace clustering on topological manifold. Adv. Neural. Inf. Process. Syst. 35, 25883–25894 (2022)
Qiang, Q., Zhang, B., Wang, F., Nie, F.: Multi-view discrete clustering: a concise model. IEEE Trans. Pattern Anal. Mach. Intell. 45(12), 15154–15170 (2023)
Bertsekas, D.P.: Nonlinear programming. J. Oper. Res. Soc. 48(3), 334–334 (1997)
Huang, J., Nie, F., Huang, H.: A new simplex sparse learning model to measure data similarity for clustering. In: 24th International Joint Conference on Artificial Intelligence (2015)
Huang, S., Tsang, I., Xu, Z., Lv, J., Liu, Q.H.: Multi-view clustering on topological manifold. In: AAAI Conference on Artificial Intelligence, vol. 36, pp. 6944–6951 (2022)
Wang, H., Yang, Y., Liu, B., Fujita, H.: A study of graph-based system for multi-view clustering. Knowl. Based Syst. 163, 1009–1019 (2019)
Tan, Y., Liu, Y., Huang, S., Feng, W., Lv, J.: Sample-level multi-view graph clustering. In: IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 23966–23975 (2023)
Ng, A., Jordan, M.: On spectral clustering: analysis and an algorithm. Adv. Neural Inf. Process. Syst. 14, (2001)
Sun, M., Zhang, P., Wang, S., Zhou, S., Tu, W., Liu, X., Zhu, E., Wang, C.: Scalable multi-view subspace clustering with unified anchors. In: 29th ACM International Conference on Multimedia (2021)
Wang, S., Liu, X., Zhu, X., Zhang, P., Zhang, Y., Gao, F., Zhu, E.: Fast parameter-free multi-view subspace clustering with consensus anchor guidance. IEEE Trans. Image Process. 31, 556–568 (2021)
Huang, S., Ren, Y., Xu, Z.: Robust multi-view data clustering with multi-view capped-norm k-means. Neurocomputing 311, 197–208 (2018)
Xu, J., Han, J., Nie, F.: Discriminatively embedded k-means for multi-view clustering. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 5356–5364 (2016)
Zhan, K., Zhang, C., Guan, J., Wang, J.: Graph learning for multiview clustering. IEEE Trans. Cybern. 48(10), 2887–2895 (2017)
He, W.J., Zhang, Z.: Adaptive topological graph learning for generalized multi-view clustering. In: International Joint Conference on Neural Networks (IJCNN), pp. 1–8 (2023)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC) under Grant No. 62306234, 62201452, the Natural Science Basic Research Program of Shaanxi (Program No. 2024JC-YBQN-0643), the Special Scientific Research Program of Education Department of Shaanxi (No. 22JK0562), and NPU ASGO Lab.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2025 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Shi, S., Liu, Y., Zhang, C., Chen, X. (2025). Multi-view Spectral Clustering Based on Topological Manifold Learning. In: Lin, Z., et al. Pattern Recognition and Computer Vision. PRCV 2024. Lecture Notes in Computer Science, vol 15031. Springer, Singapore. https://doi.org/10.1007/978-981-97-8487-5_18
Download citation
DOI: https://doi.org/10.1007/978-981-97-8487-5_18
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-97-8486-8
Online ISBN: 978-981-97-8487-5
eBook Packages: Computer ScienceComputer Science (R0)