Abstract
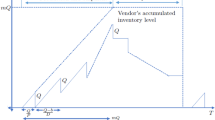
In this article, an integrated single-vendor single-buyer imperfect production–inventory model in which the vendor makes investment for process quality improvement and the buyer offers price discounts for backorders is studied. It is assumed that the buyer follows a continuous review policy with lot-size-dependent lead-time and a mixture of backorders and lost sales. Under the n-shipment policy, the expected annual total cost of the integrated system is derived. An algorithm is developed to determine numerically the optimal decisions of the model. A numerical example is taken to illustrate the developed model and to examine the sensitivity of the key parameters of the model. Some managerial insights are also provided.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Banerjee, A.: A joint economic-lot-size model for purchaser and vendor. Decis. Sci. 17, 292–311 (1986)
Ben-Daya, M., Hariga, M.: Economic lot scheduling problem with imperfect production process. J. Oper. Res. Soc. 51, 875–881 (2000)
Ben-Daya, M., Hariga, M.: Integrated single vendor single buyer model with stochastic demand and variable lead-time. Int. J. Prod. Econ. 92, 75–80 (2004)
Dey, O., Giri, B.C.: Optimal vendor investment for reducing defect rate in a vendor?buyer integrated system with imperfect production process. Int. J. Prod. Econ. 155, 222–228 (2014)
Glock, C.H.: A comment: integrated single vendor-single buyer model with stochastic demand and variable lead time. Int. J. Prod. Econ. 122, 790–792 (2009)
Glock, C.H.: Lead timer eduction strategies in a single-vendorsingle-buyer integrated inventory model with lot size-dependent lead times and stochastic demand. Int. J. Prod. Econ. 136, 37–44 (2012)
Goyal, S.K.: An integrated inventory model for a single supplier-single customer problem. Int. J. Prod. Res. 15, 107–111 (1976)
Goyal, S.K.: A joint economic-lot-size model for purchaser and vendor: a comment. Decis. Sci. 19, 236–241 (1988)
Goyal-Cardenas-Barron, L.E.: The economic production quantity (EPQ) with shortage derived algebraically. Int. J. Prod. Econ. 70, 289–292 (2002)
Ha, D., Kim, S.L.: Implementation of JIT purchasing: an integrated approach. Prod. Plan. Control. 8, 152–157 (1997)
Hill, R.M.: The optimal production and shipment policy for the single-vendor single-buyer integrated production-inventory problem. Int. J. Prod. Res. 37, 2463–2475 (1999)
Hsiao, Y.-C.: Integrated logistic and inventory model for a two-stage supply chain controlled by the reorder and shipping points with sharing information. Int. J. Prod. Econ. 115, 229–235 (2008)
Huang, C.K.: An optimal policy for a single-vendor single-buyer integrated production-inventory problem with process unreliability consideration. Int. J. Prod. Econ. 91, 91–98 (2004)
Jaggi, C.K., Arneja, N.: Periodic inventory model with unstable lead-time and set-up cost with backorder price discount. Int J. Appl. Decis. Sci. 3(1), 53–73 (2010)
Jauhari, W.A.: Lot size decisions for vendor-buyer system with quantity discount, partial backorder and stochastic demand. Adv. Oper. Res. Article ID-597626, 7p (2014)
Jindal, P.A.S.: Integrated supply chain inventory model with quality improvement involving controllable lead-time and Backorder price discount. Int. J. Ind. Eng. Comput. 7(3), 463–480 (2016). https://doi.org/10.5267/j.ijec.2015.12.003
Lin, Y.-J.: An integrated vendor-buyer inventory model with backorder price discount and effective investment to reduce ordering cost. Comput. Ind. Eng. 56, 1597–1606 (2009)
Lin, H.J.: An integrated supply chain inventory model with imperfect-quality items, controllable lead time demand and distribution-free demand. Yugoslav J. Oper. Res. 23, 87–109 (2013)
Ouyang, L.Y., Wu, K.S., Ho, C.H.: Analysis of optimal vendor-buyer integrated inventory policy involving defective items. Int. J. Adv. Manuf. Technol. 29, 1232–1245 (2006)
Pal, M., Chandra, S.: Aperiodic review inventory model with stock dependent demand,permissible delay in payment and price discounts on backorder. Yugoslav J. Oper. Res. 24(1), 99–110 (2012). https://doi.org/10.2298/YJOR120512017P
Pan, J.C.H., Yang, J.S.: A study of an integrated inventory with controllable lead time. Int. J. Prod. Res. 40, 1263–1273 (2002)
Porteus, E.L.: Optimal lot sizing, process quality improvement and setup cost reduction. Oper. Res. 36, 137–144 (1986)
Rosenblatt, M.J., Lee, H.L.: Economic production cycles with imperfect production process. IIE Trans. 18, 48–55 (1986)
Yang, J.S., Pan, C.H.J.: Just-in-time purchasing: an integrated inventory model involving deterministic variable lead time and quality improvement investment. Int. J. Prod. Res. 42(5), 853–863 (2004)
Zhang, X., Gerchak, Y.: Joint lot sizing and inspection policy in an EOQ model with random yield. IIE Trans. 22, 41–47 (1990)
Further Reading
Jana, D.K., Chakraborty, D., Maiti, M.: A random fuzzy production inventory problem with backorder rate based on controllable preparation time and safety factor via genetic algorithm
Jana, D.K., Maity, K., Roy, T.K.: Multi-objective imperfect production inventory model in fuzzy rough environment via genetic algorithm
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Mukherjee, A., Dey, O., Giri, B.C. (2019). An Integrated Imperfect Production–Inventory Model with Optimal Vendor Investment and Backorder Price Discount. In: Chandra, P., Giri, D., Li, F., Kar, S., Jana, D. (eds) Information Technology and Applied Mathematics. Advances in Intelligent Systems and Computing, vol 699. Springer, Singapore. https://doi.org/10.1007/978-981-10-7590-2_14
Download citation
DOI: https://doi.org/10.1007/978-981-10-7590-2_14
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-7589-6
Online ISBN: 978-981-10-7590-2
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)