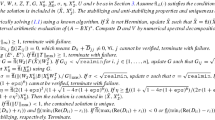Abstract
In this note we describe a new method to calculate verified solutions of the matrix Riccati equation (ARE) with interval coefficients. Such an equation has to be solved when we want to find the steady state solutions of matrix Riccati differential equation with constant coefficients which arises in the theory of automatic control and linear filtering.
Given the Riccati polynomial P(X) we use the Fréchet-derivative at X to derive a linear equation of type CX + XD = P. Applying Brouwer’s fixed point theorem, we find an interval matrix [X] that includes a positive definite solution of the equation P(X) = Ω.
First we want to give an outline of linear-quadratic control theory. Then we present results concerning the geometric structures of all solutions and enumerate linearly and quadratically convergent algorithms to find a solution used to construct the optimal feedback control for linear-quadratic optimal control problems.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Alefeld, G. and Meyer, G. The Cholesky method for interval data. Linear Algebra Appl., 194: 161–182, 1994.
Armstrong, E. S. An extension of Bass’ algorithm for stabilizing linear continuous constant systems. IEEE Trans. Automat. Control, AC-20(4): 153–154, 1975.
Bunse—Gerstner, A., Byers, R. and Mehrmann, V. Numerical methods for algebraic Riccati equations. In S. Bittanti, editor, Lecture Notes of the Workshop on “The Riccati Equation in Control, Systems, and Signals”, (Como, Italy), pages 107–115. Pitagora Editrice, Bologna, 1989.
Freiling, G. and Jank, G. Non—symmetric matrix Riccati equations. J. Analysis Appl., 14: 259284, 1995.
Jansson, C. Interval linear systems with symmetric matrices, skew-symmetric matrices and dependencies in right hand side. Computing, 46: 265–274, 1991.
Knüppel, O. ProfiUBIAS — A fast interval library. Computing, 53: 277–287, 1994.
Kratz, W. and Stickel, E. Numerical solution of matrix polynomial equations by Newton’s method. IMA J. blunter. Anal., 7: 355–369, 1987.
Luther, W. and Otten, W. The complex arithmetic geometric mean and multiple—precision matrix functions. In Alefeld, G., Frommer, A, and Lang, B., editor, Scientific Computing and Validated Numerics, Proceedings of SCAN-95, pages 52–58. Akademie Verlag, Berlin, 1996.
Mehrmann, V. and Tan, E. Defect correction methods for the solution of algebraic Riccati equations. IEEE Trans. Automat. Control, AC-33(7): 695–698, 1988.
Potter, J. E. Matrix quadratic solutions. J. SIAM Appi. Math., 14: 496–501, 1966.
Rump, S. M. Improved iteration schemes for the validation algorithms for dense and sparse nonlinear systems. Computing, 57: 77–84, 1996.
Shayman, M. A. Geometry of the algebraic Riccati equation, part I and part II. SIAM J. Control and Optimization, 21: 375–394, 395–409, 1983.
Sima, V. Algorithms for linear—quadratic optimization. Marcel Dekker, New York, 1996.
Willems, J. C. Least squares stationary optimal control and the algebraic Riccati equation. IEEE Trans. Autom. Control, AC-16: 621–634, 1971.
Zurmühl, R. and Falk, S. Matrizen and ihre Anwendungen. Springer, Berlin, 1984.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1999 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Luther, W., Otten, W. (1999). Verified calculation of the solution of algebraic Riccati equation. In: Csendes, T. (eds) Developments in Reliable Computing. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-1247-7_8
Download citation
DOI: https://doi.org/10.1007/978-94-017-1247-7_8
Publisher Name: Springer, Dordrecht
Print ISBN: 978-90-481-5350-3
Online ISBN: 978-94-017-1247-7
eBook Packages: Springer Book Archive