Extraction of Crack-free Isosurfaces from Adaptive Mesh Refinement Data | SpringerLink
Skip to main content
Springer Nature Link
Log in

Extraction of Crack-free Isosurfaces from Adaptive Mesh Refinement Data

  • Conference paper
Data Visualization 2001

Part of the book series: Eurographics ((EUROGRAPH))

Abstract

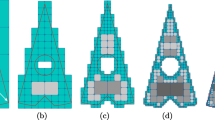
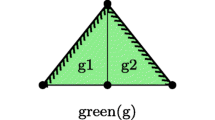
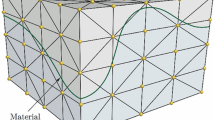
Adaptive mesh refinement (AMR) is a numerical simulation technique used in computational fluid dynamics (CFD). It permits the efficient simulation of phenomena characterized by substantially varying scales in complexity of local behavior of certain variables. By using a set of nested grids at different resolutions, AMR combines the simplicity of structured rectilinear grids with the possibility to adapt to local changes in complexity and spatial resolution. Hierarchical representations of scientific data pose challenges when isosurfaces are extracted. Cracks can arise at the boundaries between regions represented at different resolutions. We present a method for the extraction of isosurfaces from AMR data that avoids cracks at the boundaries between levels of different resolution.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 5719
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 7149
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. AVS5. Product of Advanced Visual Systems, further details can be found at http://www.avs.com/products/AVS5/avs5.htm.

  2. Marsha Berger and Phillip Colella. Local adaptive mesh refinement for shock hydrodynamics. Journal of Computational Physics, 82:64–84, May 1989. Lawrence Livermore National Laboratory, Technical Report No. UCRL-97196.

    Article  MATH  Google Scholar 

  3. Marsha Berger and Joseph Oliger. Adaptive mesh refinement for hyperbolic partial differential equations. Journal of Computational Physics, 53:484–512, March 1984.

    Article  MathSciNet  MATH  Google Scholar 

  4. Greg L. Bryan. Fluids in the universe: Adaptive mesh refinement in cosmology. Computing in Science and Engineering, 1(2):46–53, March/April 1999.

    Article  MathSciNet  Google Scholar 

  5. Allen Van Gelder and Jane Wilhelms. Topological considerations in isosurface generation. ACM Transactions on Graphics, 13(4):337–375, October 1994.

    Article  Google Scholar 

  6. Markus B. Gross, Oliver G. Staadt, and Roger Gatti. Efficient triangular surface approximations using wavelets and quadtree data structures. IEEE Transactions on Visualization and Computer Graphics, 2(2):130–143, June 1996.

    Article  Google Scholar 

  7. Interactive Data Language (IDL). Product of Research Systems, Inc., see http://www.rsine.com/idl/index.cfm for details.

  8. William E. Lorensen and Harvey E. Cline. Marching cubes: A high resolution 3D surface construction algorithm. Computer Graphics (SIGGRAPH’ 87 Proceedings), 21(4):163–169, July 1987.

    Article  Google Scholar 

  9. Kwan-Liu Ma. Parallel rendering of 3D AMR data on the SGI/Cray T3E. In: Proceedings of Frontiers’ 99 the Seventh Symposium on the Frontiers of Massively Parallel Computation, pages 138–145, IEEE Computer Society Press, Los Alamitos, California, February 1999.

    Chapter  Google Scholar 

  10. Nelson L. Max. Sorting for polyhedron compositing. In: Hans Hagen, Heinrich Müller, and Gregory B. Nielson, editors, Focus on Scientific Visualization, pages 259–268. Springer-Verlag, New York, New York, 1993.

    Chapter  Google Scholar 

  11. Gregory M. Nielson and Bernd Hamann. The asymptotic decider: Removing the ambiguity in marching cubes. In: Gregory M. Nielson and Larry J. Rosenblum, editors, IEEE Visualization’ 91, pages 83–91, IEEE Computer Society Press, Los Alamitos, California, 1991.

    Chapter  Google Scholar 

  12. Michael L. Norman, John M. Shalf, Stuart Levy, and Greg Daues. Diving deep: Data management and visualization strategies for adaptive mesh refinement simulations. Computing in Science and Engineering, 1(4):36–47, July/August 1999.

    Article  Google Scholar 

  13. William J. Schroeder, Kenneth M. Martin, and William E. Lorensen. The Visualization Toolkit, second edition, 1998. Prentice-Hall, Upper Saddle River, New Jersey.

    Google Scholar 

  14. Raj Shekhar, Elias Fayyad, Roni Yagel, and J. Fredrick Cornhill. Octree-based decimation of marching cubes surface. In: Roni Yagel and Gregory M. Nielson, editors, IEEE Visualization’ 96, pages 335–342, 499, IEEE Computer Society Press, Los Alamitos, California, October 1998.

    Google Scholar 

  15. Rüdiger Westermann, Leif Kobbelt, and Thomas Ertl. Real-time exploration of regular volume data by adaptive reconstruction of iso-surfaces. The Visual Computer, 15(2):100–111, 1999.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Image Processing and Integrated Computing (CIPIC), Department of Computer Science, University of California, Davis, USA

    Guther H. Weber, Oliver Kreylos, Bernd Hamann & Kenneth I. Joy

  2. Department of Computer Science, University of Kaiserslautern, Germany

    Guther H. Weber, Oliver Kreylos & Hans Hagen

  3. National Energy Research Scientific Computing Center (NERSC), Lawrence Berkeley National Laboratory, Berkeley, USA

    Guther H. Weber, Terry J. Ligocki, John M. Shalf & Bernd Hamann

  4. National Center for Supercomputing Applications (NCSA), University of Illinois, Urbana-Champaign, USA

    John M. Shalf

Authors
  1. Guther H. Weber
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Oliver Kreylos
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Terry J. Ligocki
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. John M. Shalf
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hans Hagen
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Bernd Hamann
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Kenneth I. Joy
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. School of Electrical and Computer Engineering, Purdue University, West Lafayette, USA

    David S. Ebert

  2. Data Mining & Visualization, CSCS, Manno, Switzerland

    Jean M. Favre

  3. Institut für wissenschaftliches Rechnen, ETH-Zentrum, IFW, Zürich, Switzerland

    Ronald Peikert

Rights and permissions

Reprints and permissions

Copyright information

© 2001 Springer-Verlag Wien

About this paper

Cite this paper

Weber, G.H. et al. (2001). Extraction of Crack-free Isosurfaces from Adaptive Mesh Refinement Data. In: Ebert, D.S., Favre, J.M., Peikert, R. (eds) Data Visualization 2001. Eurographics. Springer, Vienna. https://doi.org/10.1007/978-3-7091-6215-6_4

Download citation

  • DOI: https://doi.org/10.1007/978-3-7091-6215-6_4

  • Publisher Name: Springer, Vienna

  • Print ISBN: 978-3-211-83674-3

  • Online ISBN: 978-3-7091-6215-6

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation