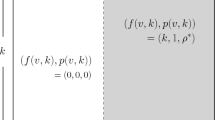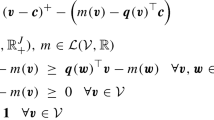Abstract
We provide sufficient conditions for revenue maximization in a two-good monopoly where the buyer’s valuations for the items come from independent (but not necessarily identical) distributions over bounded intervals. Under certain distributional assumptions, we give exact, closed-form formulas for the prices and allocation rules of the optimal selling mechanism. As a side result we give the first example of an optimal mechanism in an i.i.d. setting over a support of the form [0, b] which is not deterministic. Since our framework is based on duality techniques, we were also able to demonstrate how slightly relaxed versions of it can still be used to design mechanisms that have very good approximation ratios with respect to the optimal revenue, through a “convexification” process.
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 321171.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Babaioff, M., Immorlica, N., Lucier, B., Weinberg, S.M.: A simple and approximately optimal mechanism for an additive buyer. In FOCS 2014 (2014)
Daskalakis, C., Deckelbaum, A., Tzamos, C.: The complexity of optimal mechanism design. In: SODA 2013, pp. 1302–1318 (2013)
Daskalakis, C., Deckelbaum, A., Tzamos, C.: Mechanism design via optimal transport. In: EC 2013, pp. 269–286 (2013)
Giannakopoulos, Y.: Bounding the optimal revenue of selling multiple goods. CoRR, abs/1404.2832 (2014)
Giannakopoulos, Y., Koutsoupias, E.: Duality and optimality of auctions for uniform distributions. In: EC 2014, pp. 259–276 (2014)
Hart, S., Nisan, N.: Approximate revenue maximization with multiple items. In: EC 2012 (2012)
Hart, S., Nisan, N.: The menu-size complexity of auctions. In: EC 2013, pp. 565–566 (2013)
Hart, S., Reny, P.J.: Maximal revenue with multiple goods: nonmonotonicity and other observations. Technical report, The Center for the Study of Rationality, Hebrew University, Jerusalem (2012)
Li, X., Yao, A.C.-C.: On revenue maximization for selling multiple independently distributed items. Proc. Natl. Acad. Sci. 110(28), 11232–11237 (2013)
Lovász, L., Plummer, M.D.: Matching theory, North-Holland (1986)
Manelli, A.M., Vincent, D.R.: Bundling as an optimal selling mechanism for a multiple-good monopolist. J. Econ. Theory 127(1), 1–35 (2006)
McAfee, R.P., McMillan, J.: Multidimensional incentive compatibility and mechanism design. J. Econ. Theory 46(2), 335–354 (1988)
Myerson, R.B.: Optimal auction design. Mathematics of Operations Research 6(1), 58–73 (1981)
Ore, O.: Graphs and matching theorems. Duke Mathematical Journal 22(4), 625–639 (1955)
Pavlov, G.: Optimal mechanism for selling two goods. The BE Journal of Theoretical Economics 11(1) (2011)
Rochet, J.-C.: The taxation principle and multi-time hamilton-jacobi equations. Journal of Mathematical Economics 14(2), 113–128 (1985)
Wang, Z., Tang, P.: Optimal mechanisms with simple menus. In: EC 2014 (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Giannakopoulos, Y., Koutsoupias, E. (2015). Selling Two Goods Optimally. In: Halldórsson, M., Iwama, K., Kobayashi, N., Speckmann, B. (eds) Automata, Languages, and Programming. ICALP 2015. Lecture Notes in Computer Science(), vol 9135. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-47666-6_52
Download citation
DOI: https://doi.org/10.1007/978-3-662-47666-6_52
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-47665-9
Online ISBN: 978-3-662-47666-6
eBook Packages: Computer ScienceComputer Science (R0)