Boosted Bellman Residual Minimization Handling Expert Demonstrations

Abstract

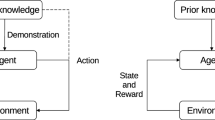
This paper addresses the problem of batch Reinforcement Learning with Expert Demonstrations (RLED). In RLED, the goal is to find an optimal policy of a Markov Decision Process (MDP), using a data set of fixed sampled transitions of the MDP as well as a data set of fixed expert demonstrations. This is slightly different from the batch Reinforcement Learning (RL) framework where only fixed sampled transitions of the MDP are available. Thus, the aim of this article is to propose algorithms that leverage those expert data. The idea proposed here differs from the Approximate Dynamic Programming methods in the sense that we minimize the Optimal Bellman Residual (OBR), where the minimization is guided by constraints defined by the expert demonstrations. This choice is motivated by the the fact that controlling the OBR implies controlling the distance between the estimated and optimal quality functions. However, this method presents some difficulties as the criterion to minimize is non-convex, non-differentiable and biased. Those difficulties are overcome via the embedding of distributions in a Reproducing Kernel Hilbert Space (RKHS) and a boosting technique which allows obtaining non-parametric algorithms. Finally, our algorithms are compared to the only state of the art algorithm, Approximate Policy Iteration with Demonstrations (APID) algorithm, in different experimental settings.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.