Abstract
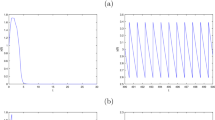
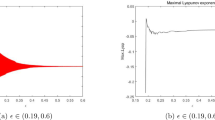
In this paper, impulsive multi-species semi-ratio-dependent predator-prey system with functional responses is investigated. Sufficient conditions for existence of a positive periodic solution can be obtained by using a continuation theorem in coincidence degree theory. Some numerical simulations show that our system can occur many forms of complexities including chaotic strange attractor and periodic solution. Sufficient criteria are established for the global stability of the system by using the comparison principle and the Lyapunov method.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Fan, X., Wang, Z., Luo, Z.: Persistence and periodic solutions fornonautonomous predator-prey systemwith functional responses and invest rate. Math. Practice Theory 38, 123–130 (2008)
Yan, X., Zhang, C.: Asymptotic stability of positive equilibrium solution for a delayed prey-predator diffusion system. Appl. Math. Model. 34, 184–199 (2010)
Ji, C., Jiang, D., Shi, N.: Analysis of a predator-preymodelwithmodified Leslie-Gower and Holling-type II schemeswith stochastic perturbation. J. Math. Anal. Appl. 359, 482–498 (2009)
Lai, W.Y., Zhan, Q.Y.: Permanence and Global Stability of a Predator-prey System with Stage Structure and Time Delays. College Mathematics 28, 50–57 (2012)
Ding, X.Q., Su, B.T., Hao, J.M.: Positive periodic solutions for impulsive Gause-type predatorCprey systems. Applied Mathematics and Computation 218, 6785–6797 (2012)
Sivasundaram, S., Vassilyev, S.: Stability and attractivity of solutions of differential equations with impulses at fixed times. J. Appl. Math. Stoch. Anal. 13, 77–84 (2000)
Wang, S.B., Huang, T.W., Kuang, Y.: A ratio-dependent food chain model and its applications to biological control. Mathematical Biosciences 181, 55–83 (2003)
Tineo, A.: Permanence of a large class of periodic predator-prey systems. J. Math. Anal. Appl. 241, 83–91 (2000)
Ahmad, S., Stamova, I.M.: Asymptotic stability of an N-dimensional impulsive competitive system. Nonlinear Anal. RealWorld Appl. 8, 654–663 (2007)
Gaines, R.E., Mawhin, J.L.: Coincidence Degree and Nonlinear Differential Equations. Springer, Berlin (1977)
Zhang, W.X., Wang, K.H., Gui, Z.J.: Periodic solution of semi-ratio-dependent predator-prey system with Holling type III functional response and impulsive effect. In: 5th International Congress on Mathematical Biology, pp. 92–97. World Academic Press (2011)
Zhang, J., Gui, J.: Periodic solutions of nonautonomous cellular neural networks with impulses and delays. Nonlinear Analysis: Real World Applications 19, 1891–1903 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Zhang, W., Gui, Z., Wang, K. (2012). Dynamics and Simulations of Impulsive Semi-Ratio-Dependent Predator-Prey System with Functional Responses. In: Liu, C., Wang, L., Yang, A. (eds) Information Computing and Applications. ICICA 2012. Communications in Computer and Information Science, vol 308. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-34041-3_76
Download citation
DOI: https://doi.org/10.1007/978-3-642-34041-3_76
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-34040-6
Online ISBN: 978-3-642-34041-3
eBook Packages: Computer ScienceComputer Science (R0)