Abstract
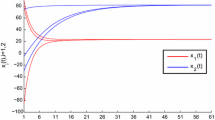
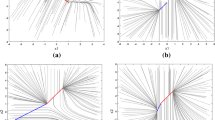
This paper is concerned with the dynamical stability analysis of multiple equilibrium points in recurrent neural networks with piecewise linear nondecreasing activation functions. By a geometrical observation, conditions are obtained to ensure that n-dimensional recurrent neural networks with r-stair piecewise linear nondecreasing activation functions can have (2r + 1)n equilibrium points. Positively invariant regions for the solution flows generated by the system are established. It is shown that this system can have (r + 1)n locally exponentially stable equilibrium points located in invariant regions. Moreover, the result is presented that there exist (2r + 1)n − (r + 1)n unstable equilibrium points for the system. Finally, an example is given to illustrate the effectiveness of the results.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Morita, M.: Associative memory with non-monotone dynamics. Neural Networks 6(1), 115–126 (1993)
Yi, Z., Tan, K.: Multistability of Discrete-Time Recurrent Neural Networks With Unsaturating Piecewise Linear Activation Functions. IEEE Transactions on Neural Networks 15(2), 329–336 (2004)
Zhang, L., Yi, Z., Yu, J.: Multiperiodicity and Attractivity of Delayed Recurrent Neural Networks With Unsaturating Piecewise Linear Transfer Functions. IEEE Transactions on Neural Networks 19(1), 158–167 (2008)
Zhang, L., Yi, Z., Yu, J., Heng, P.A.: Some multistability properties of bidirectional associative memory recurrent neural networks with unsaturating piecewise linear transfer functions. Neurocomputing 72(13-15), 3809–3817 (2009)
Zhang, L., Yi, Z., Yu, J., Heng, P.A.: Activity Invariant Sets and Exponentially Stable Attractors of Linear Threshold Discrete-Time Recurrent Neural Networks. IEEE Transactions on Automatic Control 54(6), 1341–1347 (2009)
Cheng, C., Lin, K., Shih, C.: Multistability in recurrent neural networks. SIAM Journal on Applied Mathematics 66(4), 1301–1320 (2006)
Cheng, C., Lin, K., Shih, C.: Multistability and convergence in delayed neural networks. Physica D: Nonlinear Phenomena 225(1), 61–64 (2007)
Huang, G., Cao, J.: Multistability in bidirectional associative memory neural networks. Physics Letters A 372(16), 2842–2854 (2008)
Cao, J., Feng, G., Wang, Y.: Multistability and multiperiodicity of delayed Cohen-Grossberg neural networks with a general class of activation functions. Physica D: Nonlinear Phenomena 237(13), 1734–1749 (2008)
Huang, Y., Zhang, X.: Multistability properties of linear threshold discrete-time recurrent neural networks. International Journal of Information and Systems Sciences 7(1), 1–10 (2010)
Chen, T., Amari, S.: New theorems on global convergence of some dynamical systems. Neural Networks 14(4), 251–255 (2001)
Wang, L., Lu, W., Chen, T.: Multistability and new attraction basins of almost periodic solutions of delayed neural networks. IEEE Transactions on Neural Networks 20(3), 1581–1593 (2009)
Wang, L., Lu, W., Chen, T.: Coexistence and local stability of multiple equilibria in neural networks with piecewise linear nondecreasing activation functions. Neural Networks 23(2), 189–200 (2010)
Zeng, Z., Huang, D., Wang, Z.: Memory pattern analysis of cellular neural networks. Physics Letters A 342(1-2), 114–128 (2005)
Zeng, Z., Wang, J.: Multiperiodicity of discrete-time delayed neural networks evoked by periodic external inputs. IEEE Transactions on Neural Networks 17(5), 1141–1151 (2006)
Zeng, Z., Wang, J.: Multiperiodicity and exponential attractivity evoked by periodic external inputs in delayed cellular neural networks. Neural Computation 18(4), 848–870 (2006)
Zeng, Z., Huang, T., Zheng, W.: Multistability of Recurrent Neural Networks with Time-varying Delays and the Piecewise Linear Activation Function. IEEE Transactions on Neural Networks 21(8), 1371–1377 (2010)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Huang, Y., Zhang, H., Wang, Z., Zhao, M. (2012). Stability Analysis of Multiple Equilibria for Recurrent Neural Networks. In: Wang, J., Yen, G.G., Polycarpou, M.M. (eds) Advances in Neural Networks – ISNN 2012. ISNN 2012. Lecture Notes in Computer Science, vol 7367. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-31346-2_23
Download citation
DOI: https://doi.org/10.1007/978-3-642-31346-2_23
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-31345-5
Online ISBN: 978-3-642-31346-2
eBook Packages: Computer ScienceComputer Science (R0)