Abstract
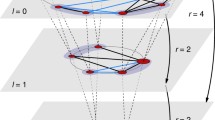
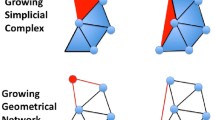
Some results by Krioukov et al. show how real world networks are produced by hidden metric spaces. Specifically, scale-free networks can be obtained from hyperbolic metric spaces. While the model proposed by Krioukov can produce a static scale-free network, all nodes are created at one time and none can be later added. In this work we propose a growing model which leverages the same concepts and allows to gradually add nodes to a scale-free network, obtained from a discretised hyperbolic model. We also show how nodes are correctly positioned relying on local information and how greedy routing builds optimal paths in the network.
This work was carried out when Antonio Lima was at the DIEEI, University of Catania.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Albert, R., Barabási, A.-L.: Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002)
Anderson, J.W.: Hyperbolic Geometry. Springer, London (2005)
Barabasi, A.-L.: Scale-free networks: A decade and beyond. Science 325(5939), 412–413 (2009)
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., Hwang, D.-U.: Complex networks: Structure and dynamics. Physics Reports 424(4-5), 175–308 (2006)
Kleinberg, J.M.: Navigation in a small world. Nature 406(6798) (August 2000)
Kleinberg, J.M.: Complex networks and decentralized search algorithms. In: ICM (2006)
Krioukov, D., Papadopoulos, F., Boguñá, M., Vahdat, A.: Efficient navigation in scale-free networks. Embedded in Hyperbolic Metric Spaces (2008) arXiv:0805.1266v1 [cond-mat.stat-mech]
Lua, E.K., Crowcroft, J., Pias, M., Sharma, R., Lim, S.: A survey and comparison of peer-to-peer overlay network schemes. IEEE Communications Surveys and Tutorials 7, 72–93 (2005)
Newman, M.E.J.: The structure and function of complex networks. SIAM Review 45, 167 (2003)
Papadopoulos, F., Krioukov, D., Boguñá, M., Vahdat, A.: Greedy forwarding in dynamic scale-free networks embedded in hyperbolic metric spaces. In: Proceedings of INFOCOM 2010. IEEE Press, USA (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Mangioni, G., Lima, A. (2013). A Growing Model for Scale–Free Networks Embedded in Hyperbolic Metric Spaces. In: Menezes, R., Evsukoff, A., González, M. (eds) Complex Networks. Studies in Computational Intelligence, vol 424. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-30287-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-642-30287-9_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-30286-2
Online ISBN: 978-3-642-30287-9
eBook Packages: EngineeringEngineering (R0)