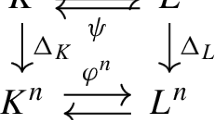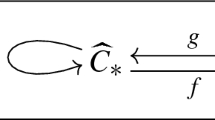
Overview
- It is the first complete exposition of the topic
- Has applications to the study of two long-standing conjectures
- It is self-contained
- Includes supplementary material: sn.pub/extras
Part of the book series: Lecture Notes in Mathematics (LNM, volume 2032)
Access this book
Tax calculation will be finalised at checkout
Other ways to access
About this book
This volume deals with the theory of finite topological spaces and its
relationship with the homotopy and simple homotopy theory of polyhedra.
The interaction between their intrinsic combinatorial and topological
structures makes finite spaces a useful tool for studying problems in
Topology, Algebra and Geometry from a new perspective. In particular,
the methods developed in this manuscript are used to study Quillen's
conjecture on the poset of p-subgroups of a finite group and the
Andrews-Curtis conjecture on the 3-deformability of contractible
two-dimensional complexes.
This self-contained work constitutes the first detailed
exposition on the algebraic topology of finite spaces. It is intended
for topologists and combinatorialists, but it is also recommended for
advanced undergraduate students and graduate students with a modest
knowledge of Algebraic Topology.
Similar content being viewed by others
Keywords
Table of contents (11 chapters)
-
Front Matter
-
Back Matter
Reviews
From the reviews:
“This book deals with the algebraic topology of finite topological spaces and its applications, and includes well-known results on finite spaces and original results developed by the author. The book is self-contained and well written. It is understandable and enjoyable to read. It contains a lot of examples and figures which help the readers to understand the theory.” (Fumihiro Ushitaki, Mathematical Reviews, March, 2014)
“This book illustrates convincingly the idea that the study of finite non-Hausdorff spaces from a homotopical point of view is useful in many areas and can even be used to study well-known problems in classical algebraic topology. … This book is a revised version of the PhD Thesis of the author. … All the concepts introduced with the chapters are usefully illustrated by examples and the recollection of all these results gives a very nice introduction to a domain of growing interest.” (Etienne Fieux, Zentralblatt MATH, Vol. 1235, 2012)
Authors and Affiliations
Bibliographic Information
Book Title: Algebraic Topology of Finite Topological Spaces and Applications
Authors: Jonathan A. Barmak
Series Title: Lecture Notes in Mathematics
DOI: https://doi.org/10.1007/978-3-642-22003-6
Publisher: Springer Berlin, Heidelberg
eBook Packages: Mathematics and Statistics, Mathematics and Statistics (R0)
Copyright Information: Springer-Verlag Berlin Heidelberg 2011
Softcover ISBN: 978-3-642-22002-9Published: 24 August 2011
eBook ISBN: 978-3-642-22003-6Published: 24 August 2011
Series ISSN: 0075-8434
Series E-ISSN: 1617-9692
Edition Number: 1
Number of Pages: XVII, 170
Number of Illustrations: 35 b/w illustrations
Topics: Algebraic Topology, Combinatorics, Convex and Discrete Geometry, Order, Lattices, Ordered Algebraic Structures, Manifolds and Cell Complexes (incl. Diff.Topology), Discrete Mathematics