Abstract
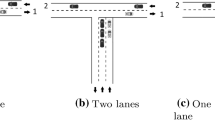
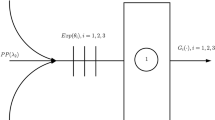
This paper considers a continuous-time queueing model with two types (classes) of customers each having their own dedicated server. The system adopts a ‘‘global FCFS’’ service discipline, i.e., all arriving customers are accommodated in one single FCFS queue, regardless of their types. As a consequence of the ‘‘global FCFS’’ rule, customers of one type may be blocked by customers of the other type, in that they may be unable to reach their dedicated server even at times when this server is idle, i.e., the system is basically non-workconserving. One major aim of the paper is to estimate the negative impact of this phenomenon on the (mean) system occupancy and mean system delay. For this reason, the systems with and without ‘‘global FCFS’’ are studied and compared. The motivation of our work are systems where this kind of blocking is encountered, such as input-queueing network switches or road splits.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Ngoduy, D.: Derivation of continuum traffic model for weaving sections on freeways. Transportmetrica 2, 199–222 (2006)
Nishi, R., Miki, H., Tomoeda, A., Nishinari, K.: Achievement of alternative configurations of vehicles on multiple lanes. Physical Review E 79, 066119 (2009)
Van Woensel, T., Vandaele, N.: Empirical validation of a queueing approach to uninterrupted traffic flows. 4OR. A Quarterly Journal of Operations Research 4, 59–72 (2006)
Van Woensel, T., Vandaele, N.: Modeling traffic flows with queueing models: A review. Asia-Pacific Journal of Operational Research 24, 435–461 (2007)
Karol, M., Hluchyj, M., Morgan, S.: Input versus output queueing on a space-division packet switch. IEEE Transactions on Communications 35, 1347–1356 (1987)
Liew, S.: Performance of various input-buffered and output-buffered ATM switch design principles under bursty traffic: simulation study. IEEE Transactions on Communications 42, 1371–1379 (1994)
Laevens, K.: A processor-sharing model for input-buffered ATM-switches in a correlated traffic environment. Microprocessors and Microsystems 22, 589–596 (1999)
Stolyar, A.: MaxWeight scheduling in a generalized switch: state space collapse and workload minimization in heavy traffic. Annals of Applied Probability 14, 1–53 (2004)
Beekhuizen, P., Resing, J.: Performance analysis of small non-uniform packet switches. Performance Evaluation 66, 640–659 (2009)
Nelson, R.: Matrix geometric solutions in Markov models: a mathematical tutorial. Technical Report RC 16777, IBM T.J. Watson Research Center, Yorktown Heights, NY (1991)
Neuts, M.F.: Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach. The John Hopkins University Press, Baltimore (1981)
Gonzáles, M.: Classical complex analysis. Marcel. Marcel Dekker, New York (1992)
Bruneel, H., Kim, B.: Discrete-time models for communication systems including ATM. Kluwer Academic Publishers, Dordrecht (1993)
Katz, V.J.: A History of Mathematics: An Introduction, 2nd edn. Addison-Wesley, Reading (1998)
Cardano, G.: Ars Magna (1545)
Kleinrock, L.: Theory, Queueing Systems, vol. 1. Wiley Interscience, Hoboken (1975)
Jackson, J.: Networks of waiting lines. Operations Research 5(4), 518–521 (1957)
Bocharov, P.P., D’Apice, C.: Queueing Theory. Walter de Gruyter, Berlin (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Mélange, W., Bruneel, H., Steyaert, B., Walraevens, J. (2011). A Two-Class Continuous-Time Queueing Model with Dedicated Servers and Global FCFS Service Discipline. In: Al-Begain, K., Balsamo, S., Fiems, D., Marin, A. (eds) Analytical and Stochastic Modeling Techniques and Applications. ASMTA 2011. Lecture Notes in Computer Science, vol 6751. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-21713-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-642-21713-5_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-21712-8
Online ISBN: 978-3-642-21713-5
eBook Packages: Computer ScienceComputer Science (R0)