Exponential Stability of Stochastic Neural Networks with Mixed Time-Delays | SpringerLink
Skip to main content
Springer Nature Link
Log in

Exponential Stability of Stochastic Neural Networks with Mixed Time-Delays

  • Conference paper
Advances in Neural Networks – ISNN 2011 (ISNN 2011)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 6675))

Included in the following conference series:

  • 1898 Accesses

Abstract

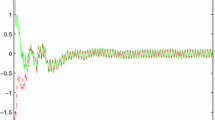
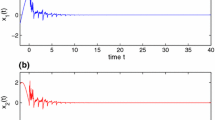
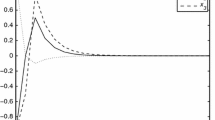
This paper investigates the exponential stability of stochastic neural networks with unbounded discrete delays and infinitely distributed delays. By using Lyapunov functions, the semi-martingale convergence theorem and some inequality techniques, the exponential stability in mean square and almost sure exponential stability are obtained. To overcome the difficulties from unbounded delays, some new techniques are introduced. Some earlier results are improved and generalized. An example is given to illustrate the results.

This research was supported by the fundamental research funds for the central universities under grant No.2010MS130.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 11439
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 14299
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Balasubramaniam, P., Rakkiyappan, R.: Global Asymptotic Stability of Stochastic Recurrent Neural Networks with Multiple Discrete Delays and Unbounded Distributed Delays. Applied Mathematics and Computation 204, 680–686 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  2. Cao, J., Yuan, K., Li, H.: Global Asymptotic Stability of Recurrent Neural Networks with Multiple Discrete Delays and Distributed Delays. IEEE Trans. Neural Networks 17, 1646–1651 (2006)

    Article  Google Scholar 

  3. Cao, J., Zhou, D.: Stability Analysis of Delayed Cellular Neural Networks. Neural Networks 11, 1601–1605 (1998)

    Article  Google Scholar 

  4. Huang, C., He, Y., Wang, H.: Mean Square Exponential Stability of Stochastic Recurrent Neural Networks with Time-varying Delays. Computers and Mathematics with Applications 56, 1773–1778 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Li, X., Fu, X.: Stability Analysis of Stochastic Functional Differential Equations with Infinite Delay and its Application to Recurrent Neural Networks. Journal of Computational and Applied Mathematics 234(2), 407–417 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  6. Liao, X., Mao, X.: Exponential Stability and Instability of Stochastic Neural Networks. Stochastic. Anal. Appl. 14(2), 165–185 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  7. Liao, X., Mao, X.: Stability of Stochastic Neural Networks. Neural, Parallel Sci. Comput. 4(2), 205–224 (1996)

    MathSciNet  MATH  Google Scholar 

  8. Liu, Y., Wang, Z., Liu, X.: Stability Criteria for Periodic Neural Networks with Discrete and Distributed Delays. Nonlinear Dyn. 4, 93–103 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. Liu, Y., Wang, Z., Liu, X.: Design of Exponential State Estimators for Neural Networks with Mixed Time Delays. Phys. Lett. A 364, 401–412 (2007)

    Article  Google Scholar 

  10. Mao, X.: Stochastic Differential Equations and Applications. Horwood, Chichester (1997)

    MATH  Google Scholar 

  11. Mohamad, S., Gopalsamy, K.: Exponential Stability of Continuous-time and Discrete-time Cellular Neural Networks with Delays. Appl. Math. Comput. 135, 17–38 (2003)

    MathSciNet  MATH  Google Scholar 

  12. Roska, T., Wu, C.W., Balsi, M., Chua, L.O.: Stability and Dynamics of Delay-type General Cellular Neural Networks. IEEE Trans. Circuit Syst. I 39(6), 487–490 (1992)

    Article  MATH  Google Scholar 

  13. Sun, Y., Cao, J.: pth Moment Exponential Stability of Stochastic Recurrent Neural Networks with Time-varying Delays. Nonlinear Analysis: Real Word Applications 8, 1171–1185 (2007)

    Article  MATH  Google Scholar 

  14. Tank, D.W., Hopfield, J.J.: Neural Computation by Concentrating Information in Time. Proc. Acad. Sci. USA 84, 1896–1900 (1987)

    Article  MathSciNet  Google Scholar 

  15. Wang, Z., Liu, Y., Liu, X.: On Global Asymptotic Stability of Neural Netwoks with Discrete and Distributed Delays. Phys. Lett. A 345, 299–308 (2005)

    Article  MATH  Google Scholar 

  16. Zeng, Z., Wang, J., Liao, X.: Global Asymptotic Stability and Global Exponential Stability of Neural Networks with Unbounded Time-varying Delays. IEEE Trans. Circuits Syst. II, Express Briefs 52(3), 168–173 (2005)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, P.R. China

    Xuejing Meng, Peng Hu & Shigeng Hu

  2. State Engineering Research Center of Numerical Control System of Huazhong University of Science and Technology, Wuhan, 430074, P.R. China

    Maosheng Tian

Authors
  1. Xuejing Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maosheng Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peng Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shigeng Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Institute of Automation, Key Laboratory of Complex Systems and Intelligence Science, Chinese Academy of Sciences, 100190, Beijing, China

    Derong Liu

  2. College of Information Science and Engineering, Shenyang, Northeastern University, 110004, Liaoing, China

    Huaguang Zhang

  3. Department of Electrical and Computer Engineering, University of Cyprus, 75 Kallipoleos Avenue, 1678, Nicosia, Cyprus

    Marios Polycarpou

  4. Dipartimento di Elettronica, Politecnico di Milano, Piazza L. da Vinci 32, 20133, Milano, Italy

    Cesare Alippi

  5. Deptartment of Electrical, Computer and Biomedical Engineering, University of Rhode Island, RI 02881, Kingston, USA

    Haibo He

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Meng, X., Tian, M., Hu, P., Hu, S. (2011). Exponential Stability of Stochastic Neural Networks with Mixed Time-Delays. In: Liu, D., Zhang, H., Polycarpou, M., Alippi, C., He, H. (eds) Advances in Neural Networks – ISNN 2011. ISNN 2011. Lecture Notes in Computer Science, vol 6675. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-21105-8_24

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-21105-8_24

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-21104-1

  • Online ISBN: 978-3-642-21105-8

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics