A Dynamic Algorithm for Reachability Games Played on Trees | SpringerLink
Skip to main content
Springer Nature Link
Log in

A Dynamic Algorithm for Reachability Games Played on Trees

  • Conference paper
Mathematical Foundations of Computer Science 2009 (MFCS 2009)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 5734))

Abstract

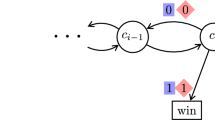
Our goal is to start the investigation of dynamic algorithms for solving games that are played on finite graphs. The dynamic game determinacy problem calls for finding efficient algorithms that decide the winner of the game when the underlying graph undergoes repeated modifications. In this paper, we focus on turn-based reachability games. We provide an algorithm that solves the dynamic reachability game problem on trees. The amortized time complexity of our algorithm is O(logn), where n is the number of nodes in the current graph.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Chatterjee, K., Henzinger, T., Piterman, N.: Algorithms for büchi games. In: Proceedings of the 3rd Workshop of Games in Design and Verification (GDV 2006) (2006)

    Google Scholar 

  2. Cormen, T., Leiserson, C., Rivest, R., Stein, C.: Introduction to algorithms, 2nd edn. MIT Press and McGraw-Hill (2001)

    Google Scholar 

  3. Demetrescu, C., Italiano, G.: Fully dynamic transitive closure: Breaking through the O(n 2) barrier. In: Proceedings of FOCS 2000, pp. 381–389 (2000)

    Google Scholar 

  4. Demetrescu, C., Italiano, G.: A new approach to dynamic all pairs shortest paths. In: Proceedings of STOC 2003, pp. 159–166 (2003)

    Google Scholar 

  5. Eppstein, D., Galil, Z., Italiano, G.: Dynamic graph algorithms. In: Atallah, M. (ed.) Algorithms and Theoretical Computing Handbook. CRC Press, Boca Raton (1999)

    Google Scholar 

  6. Grädel, E.: Model checking games. In: Proceedings of WOLLIC 2002. Electronic Notes in Theoretical Computer Science, vol. 67. Elsevier, Amsterdam (2002)

    Google Scholar 

  7. Grädel, E., Thomas, W., Wilke, T. (eds.): Automata, Logics, and Infinite Games. LNCS, vol. 2500. Springer, Heidelberg (2002)

    MATH  Google Scholar 

  8. Immerman, N.: Number of quantifiers is better than number of tape cells. Journal of Computer and System Sciences 22, 384–406 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  9. King, V.: Fully dynamic algorithms for maintaining all-pairs shortest paths and transitive closure in digraphs. In: Proceedings of FOCS 1999, pp. 81–91 (1999)

    Google Scholar 

  10. Kozen, D.: The design and analysis of algorithms. Monographs in computer science. Springer, New York (1992)

    Book  MATH  Google Scholar 

  11. Murawski, A.: Reachability games and game semantics: Comparing nondeterministic programs. In: Proceedings of LICS 2008, pp. 353–363 (2008)

    Google Scholar 

  12. Tarjan, R.: Data structures and network algorithms. Regional Conference Series in Applied Mathematics, vol. 44. SIAM, Philadelphia (1983)

    Google Scholar 

  13. Radmacher, F., Thomas, W.: A game theoretic approach to the analysis of dynamic networks. In: Proceedings of the 1st Workshop on Verification of Adaptive Systems, VerAS 2007. Electronic Notes in Theoretical Computer Science, vol. 200(2), pp. 21–37. Kaiserslautern, Germany (2007)

    Google Scholar 

  14. Rodity, L.: A faster and simpler fully dynamic transitive closure. In: Proceedings of SODA 2003, pp. 401–412 (2003)

    Google Scholar 

  15. Roditty, L., Zwick, U.: Improved dynamic reachability algorithm for directed graphs. In: Proceedings of FOCS 2002, pp. 679–689 (2002)

    Google Scholar 

  16. Roditty, L., Zwick, U.: A fully dynamic reachability algorithm for directed graphs with an almost linear update time. In: Proceedings of 36th ACM Symposium on Theory of Computing (STOC 2004), pp. 184–191 (2004)

    Google Scholar 

  17. Thomas, W.: Infinite games and verification (Extended abstract of a tutorial). In: Brinksma, E., Larsen, K.G. (eds.) CAV 2002. LNCS, vol. 2404, pp. 58–64. Springer, Heidelberg (2002)

    Chapter  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Auckland, New Zealand

    Bakhadyr Khoussainov, Jiamou Liu & Imran Khaliq

Authors
  1. Bakhadyr Khoussainov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiamou Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Imran Khaliq
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Computer Science, Faculty of Mathematics, Physics and Informatics, Comenius University, Research partially funded by grant APVV 0433-06, Bratislava, Slovakia

    Rastislav Královič

  2. Members of EACSL Jury for the Ackermann Award, Poland

    Damian Niwiński

Rights and permissions

Reprints and permissions

Copyright information

© 2009 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Khoussainov, B., Liu, J., Khaliq, I. (2009). A Dynamic Algorithm for Reachability Games Played on Trees. In: Královič, R., Niwiński, D. (eds) Mathematical Foundations of Computer Science 2009. MFCS 2009. Lecture Notes in Computer Science, vol 5734. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-03816-7_41

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-03816-7_41

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-03815-0

  • Online ISBN: 978-3-642-03816-7

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation