Abstract
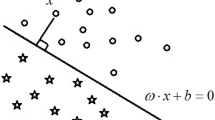
Kernel machines and rough sets are two classes of popular learning techniques. Kernel machines enhance traditional linear learning algorithms to deal with nonlinear domains by a nonlinear mapping, while rough sets introduce a human-like manner to deal with uncertainty in learning. Granulation and approximation play a central role in rough sets based learning and reasoning. Fuzzy granulation and fuzzy approximation, which is inspired by the ways in which humans granulate information and reason with it, are widely discussed in literatures. However, how to generate effective fuzzy granules from data has not been fully studied so far. In this work, we integrate kernel functions with fuzzy rough set models and propose two types of kernelized fuzzy rough sets. Kernel functions are employed to compute the fuzzy T-equivalence relations between samples, thus generate fuzzy information granules of the approximation space, and then these fuzzy granules are used to approximate the classification based on the conception of fuzzy lower and upper approximations.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Dubois, D., Prade, H.: Rough fuzzy sets and fuzzy rough sets. International Journal of General Systems 17, 191–209 (1990)
Fernandez-Riverola, F., Diaz, F., et al.: Reducing the memory size of a fuzzy case-based reasoning system applying rough set techniques. IEEE Transactions on systems man and cybernetics part c-applications and reviews 37, 138–146 (2007)
Genton, M.: Classes of kernels for machine learning: a statistics perspective. Journal of machine learning research 2, 299–312 (2001)
Guyon, I., Elisseeff, A.: An Introduction to Variable and Feature Selection. Journal of machine learning research 3, 1157–1182 (2003)
Hassanien, A.: Fuzzy rough sets hybrid scheme for breast cancer detection. Image and vision computing 25, 172–183 (2007)
Hong, T.P., Wang, T.T., Wang, S.L.: Learning a coverage set of maximally general fuzzy rules by rough sets. Expert systems with application 19, 97–103 (2000)
Hu, Q.H., Yu, D.R., Xie, Z.X.: Information-preserving hybrid data reduction based on fuzzy-rough techniques. Pattern recognition letters 27, 414–423 (2006)
Hu, Q.H., Xie, Z., Yu, D.: Hybrid attribute reduction based on a novel fuzzy-rough model and information granulation. Pattern recognition 40, 3509–3521 (2007)
Hu, Q.H., Yu, D.R., Xie, Z.X.: Neighborhood classifiers. Expert systems with applications 34, 866–876 (2008)
Jensen, R., Shen, Q.: Fuzzy-rough sets assisted attribute selection. IEEE Transactions on fuzzy systems 15, 73–89 (2007)
Kononenko, I.: Estimating attributes: Analysis and extensions of Relief. In: Bergadano, F., De Raedt, L. (eds.) ECML 1994, vol. 784, pp. 171–182. Springer, Heidelberg (1994)
Mi, J.S., Zhang, W.X.: An axiomatic characterization of a fuzzy generalization of rough sets. Information Sciences 160, 235–249 (2004)
Morsi, N.N., Yakout, M.M.: Axiomatics for fuzzy rough set. Fuzzy Sets System 100, 327–342 (1998)
Moser, B.: On the T-transitivity of kernels. Fuzzy Sets and Systems 157, 1787–1796 (2006)
Moser, B.: On representing and generating kernels by fuzzy equivalence relations. Journal of machine learning research 7, 2603–2620 (2006)
Pawlak, Z.: Rough Sets: Theoretical Aspects of Reasoning about Data. Kluwer Academic Publishers, Dordecht (1991)
Radzikowska, A.M., Kerre, E.E.: A comparative study of fuzzy rough sets. Fuzzy Sets and Systems 126, 137–155 (2002)
Shawe-Taylor, J., Cristianini, N.: Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge (2004)
Wang, X.Z., Tsang, E.C.C., Zhao, S.Y.: Learning fuzzy rules from fuzzy samples based on rough set technique. Information sciences 177, 4493–4514 (2007)
Wu, W.Z., Zhang, W.X.: Constructive and axiomatic approaches of fuzzy approximation operators. Information sciences 159, 233–254 (2004)
Yeung, D.S., Chen, D.-G., Tsang, E.C.C., Lee, J.W.T., et al.: On the generalization of fuzzy rough sets. IEEE Transactions on fuzzy systems 13, 343–361 (2005)
Zadeh, L.A.: Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets and Systems 90, 111–127 (1997)
Wu, W.-Z.: Attribute reduction based on evidence theory in incomplete decision systems. Information sciences 178, 1355–1371 (2008)
Maji, P., Pal, S.K.: Rough-fuzzy C-medoids algorithm and selection of bio-basis for amino acid sequence analysis. IEEE transactions on knowledge and data engineering 19, 859–872 (2007)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hu, Q., Chen, D., Yu, D., Pedrycz, W. (2009). Kernelized Fuzzy Rough Sets. In: Wen, P., Li, Y., Polkowski, L., Yao, Y., Tsumoto, S., Wang, G. (eds) Rough Sets and Knowledge Technology. RSKT 2009. Lecture Notes in Computer Science(), vol 5589. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02962-2_38
Download citation
DOI: https://doi.org/10.1007/978-3-642-02962-2_38
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-02961-5
Online ISBN: 978-3-642-02962-2
eBook Packages: Computer ScienceComputer Science (R0)