Abstract
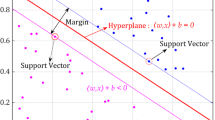
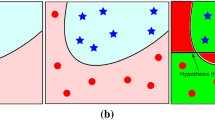
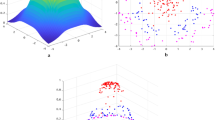
The selection of kernel function and its parameters has heavy influence on the generalization performance of support vector machine (SVM), and it becomes a focus on SVM researches. At present, there are not general rules to select an optimal kernel function for a given problem yet, alternatively, Gaussian and Polynomial kernels are commonly used for practice applications. Based on the relationship analysis of Gaussian kernel support vector machine and scale space theory, this paper proves the existence of a certain range of the parameter σ , within the range the generalization performance is good. An appropriate σ within the range can be achieved via dynamic evaluation as well. Simulation results demonstrate the feasibility and effectiveness of the presented approach.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Broomhead, D.S., Lowe, D.: Multivariable Functional Interpolation and Adaptive Networks. Complex Systems 2, 321–355 (1988)
Byun, H., Lee, S.W.: Applications of Support Vector Machines for Pattern Recognition. In: Proc. of the International Workshop on Pattern Recognition with Support vector machine, pp. 213–236. Springer, Niagara Falls (2002)
Rennie, J., Rifkin, R.: Improving Multiclass Text Classification with the Support Vector Machine. Technology Report AI Memo AIM-2001-026 and CCL Memo 210. Massachusetts Institute of Technology, MIT (October 2001)
Tsuda, K., Ratsch, G., Mika, S., et al.: Learning to Predict the Leave-One-Out Error of Kernel Based Classifiers. In: Dorffner, G., Bischof, H., Hornik, K. (eds.) ICANN 2001. LNCS, vol. 2130, pp. 331–338. Springer, Heidelberg (2001)
Seeger, M.: Bayesian Model Selection for Support Vector Machines, Gaussian Processes and Other Kernel Classifiers. In: Advances in Neural Information Systems, vol. 12, pp. 603–649. MIT Press, Cambridge (2000)
Wu, S., Amari, S.: Conformal Transformation of Kernel Functions: a Data-dependent Way to Improve Support Vector Machine Classifiers. Neural Processing Letters 15, 59–67 (2002)
Van, T.G., Sukens, J.A.K., Baestaens, D.E., et al.: Financial Time Series Prediction Using Least Squares Support Vector Machines within the Evidence Framework. IEEE Transaction on Neural Networks 12, 809–821 (2001)
Vapnik, V.: The Nature of Statistical Learning Theory. Wiley, Chichester (1995)
Wang, W.J., Xu, Z.B., Lu, W.Z., Zhang, X.Y.: Determination of the Spread Parameter in the Gaussian Kernel for Classification and Regression. Neurocomputing 55, 643–663 (2003)
Leung, Y., Zhang, J.S., Xu, Z.B.: Clustering by Scale-Space Filtering. IEEE Transaction Pattern Anal. Machine Intell. 22, 1369–1410 (2000)
Li, Y., Gong, S., Sherrah, J., Liddell, H.: Multi-View Face Detection Using Support Vector Machines and Eigenspace Modeling. In: 4th International Conference on Knowledge-Based Intelligent Engineering System and Allied Technologies, Brighton, UK, pp. 241–244 (2000)
Zhou, W.D., Zhang, L., Jiao, L.C.: An Improved Principle for Measuring Generalization Performance. Chinese Journal of Computers 26, 598–604 (2003)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wang, W., Ma, L. (2008). An Estimation of the Optimal Gaussian Kernel Parameter for Support Vector Classification. In: Sun, F., Zhang, J., Tan, Y., Cao, J., Yu, W. (eds) Advances in Neural Networks - ISNN 2008. ISNN 2008. Lecture Notes in Computer Science, vol 5263. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-87732-5_70
Download citation
DOI: https://doi.org/10.1007/978-3-540-87732-5_70
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-87731-8
Online ISBN: 978-3-540-87732-5
eBook Packages: Computer ScienceComputer Science (R0)