Association Mapping of Complex Diseases with Ancestral Recombination Graphs: Models and Efficient Algorithms

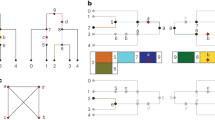
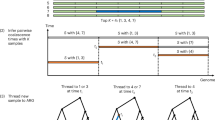
Abstract

Association, or LD (linkage disequilibrium), mapping is an intensely-studied approach to gene mapping (genome-wide or in candidate regions) that is widely hoped to be able to efficiently locate genes influencing both complex and Mendelian traits. The logic underlying association mapping implies that the best possible mapping results would be obtained if the genealogical history of the sampled individuals were explicitly known. Such a history would be in the form of an “ancestral recombination graph (ARG)”. But despite the conceptual importance of genealogical histories to association mapping, few practical association mapping methods have explicitly used derived genealogical aspects of ARGs. Two notable exceptions are [35] and [23].

In this paper we develop an association mapping method that explicitly constructs and samples minARGs (ARGs that minimize the number of recombinations). We develop an ARG sampling method that provably samples minARGs uniformly at random, and that is practical for moderate sized datasets. We also develop a different, faster, ARG sampling method that still samples from a well-defined subspace of ARGs, and that is practical for larger sized datasets. We present novel efficient algorithms on extensions of the “phenotype likelihood” problem, a key step in the method in [35]. We also prove that computing the phenotype likelihood for a different natural extension of the penetrance model in [35] is NP-hard, answering a question unresolved in that paper. Finally, we put all of these results into practice, and examine how well the implemented methods perform, compared to the results in [35]. The empirical results show great speed ups, and definite but sometimes small, improvements in mapping accuracy. Speed is particularly important in doing genome-wide scans for causative mutations.