Abstract
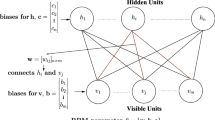
Boltzmann Machines are recurrent and stochastic neural networks that can learn and reproduce probability distributions. This feature has a serious drawback in the exhaustive computational cost involved. In this context, decimation was introduced as a way to overcome this problem, as it builds a smaller network that is able to reproduce exactly the quantities required to update the weights during learning. Decimation techniques developed can only be used in sparsely connected Boltzmann Machines with stringent constraints on the connections between the units. In this work, decimation is extended to any Boltzmann Machine with no restrictions on connections or topology. This is achieved introducing high order weights, which incorporate additional degrees of freedom.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Ackley, D.H., Hinton, G.E. and Sejnowsky, T.J., A learning algorithm for Boltzmann Machines, Cognitive Science, vol. IX, pp. 147–169, 1985.
Hinton, G.E., and Sejnowski, T.J., Learning and relearning in Boltzmann Machines, Parallel Distributed Processing, vol. I, Cambridge, M.A., U.S.A., MIT Press, pp. 282–317, 1986.
J. J. Hopfield; Neural networks and physical systems with emergent collective computational abilities, Neurocomputing: foundations of research, Cambridge, M.A., U.S.A., MIT Press, pp. 457–464, 1988.
Kirkpatrick, S., Gelatt, C.D. Jr and Vecchi, M.P., Optimization by Simulated Annealing, Science 220, pp. 671–680, 1983.
Saul, L., and Jordan, M.I., Learning in Boltzmann Trees, Neural Computation, vol. 6, num. 6, pp. 1174–1184, 1994.
Rüger, S.M., Decimatable Boltzmann Machines for Diagnosis: Efficient Learning and Inference, World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Deutschland, vol. 4, pp. 319–324, 1997.
Sejnowski, T.J., High-Order Boltzmann Machines, AIP Conference Proceedings 151 on Neural Networks for Computing, Snowbird, Utah, U.S.A., pp. 398 - 403, 1987.
Kirkpatrick, S., Gelatt, C.D. Jr. and Vecchi M.P., Optimization by simulated annealing, Neurocomputing: foundations of research, MIT Press Cambridge, MA, USA, pp. 551–567, 1988.
Aarts, E., and Korst, J., Simulated Annealing and Boltzmann Machines: a stochastic Approach to Combinatorial Optimization and Neural Computing, 3rd. ed., Great Britain, John Wiley and Sons, 1997.
Albizuri, F.X., et al., The High-Order Boltzmann Machine: Learned distribution and Topology, IEEE Transactions on Neural Networks, vol. 6, num. 3, pp. 767–770, 1995.
Kullback, S., Information theory and statistics, 2nd ed, New York, U.S.A., New York: Willey, 1959.
Itzykson, C. and Drouffe, J., Statistical field theory, Cambridge, Cambridge University Press, 1991.
ælvarez, V., et al., Matrices cocilicas de Hadamard sobre productos semidirectos, III Jornadas de Matemàtica Discreta y Algorítmica 3JMDA, Sevilla, Spain, pp. 155–158, 2002.
Assmus Jr., E. F. and Key, J. D., Hadamard matrices and their designs: a coding theorethic approach, Trans. Amer. Soc., to appear.
Park, C. H., Song, H. Y. and Park, K. T., Existence and classification of Hadamard matrices, Signal Processing Proceedings, 1998. ICSP '98, Fourth International Conference on, vol. 1, pp. 117–121, 1998.
Duda, R.O., Hart, P.E. and Stork D.G., Pattern Classification, 2nd Ed., U.S.A., Wiley-Interscience Publication, John Wiley & Sons, INC., 2001.
Li, D. et al., Studying the effects of multiplication neurons for parity problem, Proceedings of the 41st SICE Annual Conference, SICE 2002, vol.: 5, pp. 2678–2681, August 2002.
Møller, M.F., A scaled conjugate gradient algorithm for fast supervised learning, Neural Networks, vol. 6, pp. 525–533, 1993.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2007 Springer
About this chapter
Cite this chapter
Farguell, E., Mazzanti, F., Gomez-Ramirez, E. (2007). ChapBoltzmann Machines Learning Using High Order Decimation. In: Castillo, O., Melin, P., Kacprzyk, J., Pedrycz, W. (eds) Hybrid Intelligent Systems. Studies in Fuzziness and Soft Computing, vol 208. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-37421-3_2
Download citation
DOI: https://doi.org/10.1007/978-3-540-37421-3_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-37419-0
Online ISBN: 978-3-540-37421-3
eBook Packages: EngineeringEngineering (R0)