Abstract
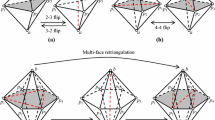
Local transformation, or topological reconnection, is one of effective procedures of mesh improvement method, especially for three-dimensional tetrahedral mesh. Although the existing local transformations such as 2-3/3-2 flip are effective in removing poorly-shaped tetrahedra, it is still possible to improve the quality of mesh further by expanding the space of transformation region. The authors recently proposed a new local transformation operation, small polyhedron reconnection (or SPR for abbreviating), which seeks the optimal tetrahedralization of a polyhedron with a certain number of vertexes and faces (typically composed of 20 to 40 tetrahedral elements).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
1. Zavattieri PD, Dari EA, Buscaglia GC (1996) Optimization strategies in unstructured mesh generation. Int J Numer Meth Engng, vol 39, no 12: 2055–2071
2. Lo SH (1997) Optimization of tetrahedral meshes based on element shape measures. Comput Struct, vol 63, no 5: 951–961
3. Freitag LA, Ollivier-Gooch C (1997) Tetrahedral mesh improvement using swapping and smoothing. Int J Numer Meth Engng, vol 40, no 21: 3979–4002
4. Freitag LA, Ollivier-Gooch C (2000) A cost/benefit analysis of simplicial mesh improvement techniques as measured by solution efficiency. Int J Comput Geom Appl, vol 10, no 4: 361–382
5. Sun SL, Liu JF (2003) An efficient optimization procedure for tetrahedral meshes by chaos search algorithm. J Comput Sci Technol, vol 18, no 6: 796–803
6. Chen ZJ, Tristano JR, Kwok W (2004) Construction of an objective function for optimization-based smoothing. Engineering with Computers, vol 20, no 3: 184–192
7. Alliez P, Cohen-Steiner D, Yvinec M, Desbrun M (2005) Variational tetrahedral meshing. ACM Transactions on Graphics, vol 24, no 3: 617–625
8. Joe B (1991) Construction of three-dimensional Delaunay triangulations using local transformations. Comput Aided Geom Design, vol 8: 123–142
9. Joe B (1995) Construction of 3-dimensional improved-quality triangulations using local transformations. SIAM J Sci Comput, vol 16, no 6: 1292–1307
10. George PL, Borouchaki H (2003) Back to edge flips in 3 dimensions. In: Proceedings of 12th International Meshing Roundtable, Sandia National Laboratories, pp 393–402
11. Liu JF, Sun SL, Wang DC (2005) Optimal tetrahedralization for small polyhedron: A new local transformation strategy for 3-D mesh generation and mesh improvement. Submitted to CMES: Computer Modeling In Engineering & Sciences
12. Liu JF, Sun SL, Chen YQ (2006) The algorithm and implementation of small polyhedron re-connection operation for tetrahedral mesh improvement. Submitted to ACM Transactions on Graphics
13. Moore RH, Saigal S (2005) Eliminating slivers in three-dimensional finite element models. CMES: Computer Modeling In Engineering & Sciences, vol 7, no 3: 283–291
14. Liu JF (2001) User manual of AutoMesh3D-A mesh generator for 3-D solid modeling. Technical report, Department of Mechanics and Engineering Science, Peking University (In Chinese)
15. Liu JF (1991) Automatic triangulation of n-D domains. In: Proceedings of CAD/Graphics'91, Hangzhou, China, pp 238–241
16. Liu JF (2003) Automatic mesh generation of 3-D geometric models. Acta Mech Sin, vol 19, no 3: 285–288
17. Lo SH (1991) Volume discretization into tetrahedral-II. 3D-triangulation by advancing front approach. Comput Struct, vol 39, no 5: 501–511
18. Nie CG, Liu JF, Sun SL (2003) Study on quality measures for tetrahedral mesh. Chinese Journal of Computational Mechanics, vol 20, no 5: 579–582 (in Chinese)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer
About this paper
Cite this paper
Liu, J., Sun, S. (2006). Small Polyhedron Reconnection: A New Way to Eliminate Poorly-Shaped Tetrahedra. In: Pébay, P.P. (eds) Proceedings of the 15th International Meshing Roundtable. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-34958-7_14
Download citation
DOI: https://doi.org/10.1007/978-3-540-34958-7_14
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-34957-0
Online ISBN: 978-3-540-34958-7
eBook Packages: EngineeringEngineering (R0)