Keywords

1 Introduction

Deep learning is a fast growing area in Artificial Intelligence as it has achieved remarkable success in many fields apart from the well publicised Go player - AlphaGo [1]. These fields include real time object detection [2], image classification [3] and video classification [4]. It also performed well in speech recognition [5] and natural language processing [6]. Major deep learning methods are Convolutional Neural Network, Deep Belief Network and Recurrent Neural Network. One of the problems of these deep learning methods is the configuration of the learning process because these learning algorithms are sensitive to parameters and a good performance is often the result of a good parameter combination. However finding a good combination is not a trivial task. For example the parameters in Convolutional Neural Network typically involve batch size, drop out rate, learning rate and training duration. They all can significantly impact the learning performance of deep learning on a particular task. In this study we will address this issue by introducing a hyper-heuristic approach to automatically tune these parameters. The particular problem in this study is image classification. We would like to train a deep network classifier to differentiate good quality images versus bad ones regardless the image content. The problem itself is novel.

Image Classification has been studied of many decades and is one of the key areas in computer vision. The task of image classification is to differentiate between images according to their categories. Image classification usually has a set of targets for example handwritten digits in images [7], human faces appeared on photos [8], various human behaviours captured in video image frames [3] and target objects like cars and books. However, in many real world scenarios, image quality, which is independent of image content, is also of significant importance. It is highly desirable that good photos can be separated from bad photos automatically. Bad images then could be improved or rejected from an image collection so less resources would be consumed. An extension on this is to even automatically select aesthetic images. The aim of this study is the first step, utilising deep learning to differentiate good images from images of obvious poor quality such as blurred images and noisy images. In particular the research goal of this study is to answer the following questions:

  1. 1.

    How to formulate deep learning to differentiate between images of good quality and images of bad quality without understanding the image content?

  2. 2.

    To what extend the training samples can be reduced while still maintaining good accuracy in classifying good vs bad images?

  3. 3.

    How to automatically tune the deep learning parameters to achieve good classification results?

Hence our investigation is also organised in three components. The first part is try to determine a suitable convolutional network structure as a classifier for good and bad images. Secondly, we study the impact of the training size on the classification performance. Thirdly, a hyper-heuristic approach is introduced to evolve the appropriate parameter combinations.

In Sect. 2 the image datasets are introduced. Section 3 describes the deep learning methodology while Sect. 4 describes the hyper-heuristic methodology. Section 5 shows the experiments with results. The conclusion is presented in Sect. 6.

2 Image Data Sets

In this study the well know image classification benchmark, the MNIST dataset is used to represent the good images [7]. MNIST is a standardized image collection which consists of handwritten digits from 0 to 9. Each digit is a 28\(\,\times \,\)28 pixel gray scale image. MNIST comes with a training set which consists of 60000 such images of digits and a test set which contains 10000 similar images.

A variation of MNIST dataset which is called noisy MNIST or n-MNIST, is used to represent the bad images [9]. There are three subsets of n-MNIST:

  1. 1.

    MNIST with motion blur

  2. 2.

    MNIST with additive white gaussian noise (awgn)

  3. 3.

    MNIST with AWGN and reduced contrast.

These datasets are the exact replicas of original MNIST but with additional noise. Each image in n-MNIST is also 28\(\,\times \,\)28 gray scale. There are 60000 training examples and 10000 test examples. The labels in training and test data-sets are hard encoded, e.g. each label is a \(1\,\times \,10\) vector (Figs. 1, 2, 3 and 4).

Fig. 1.
figure 1

Example of images from MNIST dataset [10]

Full size image
Fig. 2.
figure 2

Example of images from motion blur dataset.

Full size image
Fig. 3.
figure 3

Example of images from AWGN dataset

Full size image
Fig. 4.
figure 4

Example of images from additive white AWGN dataset.

Full size image

The MNIST with motion blur filter is created by imitating a motion of came by 5 pixels with an angle of 15\(^\circ \) which makes the filter a vector for horizontal and vertical motions. The MNIST with AWGN is created by introducing additive white Gaussian noise with signal to noise ratio of 9.5. The MNIST with reduced contrast and AWGN is created by introducing contrast range with AWGN with signal to noise ratio of 12 [9].

3 Deep Learning Methodology

In this study, we use the well-know convolutional neural network (CNN) through Keras and Tensorflow. Keras is a high-level neural network API which is built on top of Tensorflow. With keras, we can define models with different standalone configurable modules which then can be combined to form a neural network model. Tensorflow is a deep learning library developed by Google [11]. Tensorflow is a directed graph which consists of nodes and it also maintain and update the state of the node. Every node has zero or more input and zero or more outputs. Value flow among the node to node and values are arbitrary long arrays called tensors. An example of a tensor graph is shown in Fig. 5. That is a simple equation of cost computed as a function of rectified Linear Unit (ReLu) in which the matrix of weights W and input x are multiplied then adding a bias b.

Fig. 5.
figure 5

A Tensorflow computation graph [11]

Full size image

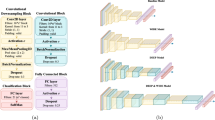
For our image classification tasks, we use two 2D convolution layers (convolution2D), with a 2D max pooling layer (MaxPooling) placed after the second convolution layer. The output of MaxPooling is flattened to a one dimensional vector which will be passed through a fully connected dense layer. The dense layer and a drop out layer are introduced after the MaxPooling2D layer to produce better generalization. For all the layers the Rectified Linear Unit (ReLu) activation is used. The output of dense layer uses the softmax activation for probabilistic classification.

The hyper-parameters of the CNN learning are listed below. The optimization target in this study is to find a good combination of these hyper-parameters and ultimately lead to a better accuracy:

  1. 1.

    The batch size - the number of training examples used in one iteration.

  2. 2.

    The number of epochs - representing the number of iteration over the entire data set.

  3. 3.

    The number of neurons in the fully connected layer.

  4. 4.

    Drop out probability.

  5. 5.

    The learning rate.

  6. 6.

    The Rho factor.

  7. 7.

    The epsilon factor.

During the learning, we split the training data into a training set and a validation set. Validation data consist of 20% of the original training set and the training set uses the rest. During training, the validation loss is monitored. When it stops decreasing or starts increasing then the training will terminate to avoid over-fitting.

Once the learning is terminated, the trained network will be applied on the test image set to obtain test accuracy. The accuracy in this study is simply classification accuracy which is calculated as

$$\begin{aligned} Accuracy\,=\,\frac{\sum {True\ Positive}\,+\,\sum {True\ Negative}}{Total\ number\ of\ Images} \end{aligned}$$
(1)

There are other ways to evaluate the model, for example ROC, F-measure and MSE. Only classification accuracy measure described above is used for simplicity reason. Also our image datasets are quite balanced and true and false cases are equally important. Hence training and test accuracies are sufficient to guide the learning and to indicate the performance of learned models.

Our second aim is to see how training size would impact the learning. It is obvious that the computational cost will be less if the training set is small. However a data set, which is too small, would not be representative enough to enable good learning. Therefore it is important to find the right balance between good performance vs computational cost, especially in real world applications. In this study we try to find minimum size for training which can still lead to reasonable test performance. Logarithmic scale is used here, in the order of \(2^n\), \(2^{n-1}\), \(2^{n-2}\), until \(2^3\) and \(2^2\).

Note the size reduction only applies on the training data. The test set, which contains 10000 MNIST images (good) and 10000 n-MNIST images (bad), is consistently used in all experiments. Only test accuracy is used to report the learning performance unless specified otherwise.

4 Hyper-heuristic Parameter Optimisation

Hyper-heuristics have been proposed for selecting and generating heuristics to solve a particular problem [12]. It has been successful in many different fields [12,13,14,15,16,17,18]. The aim of hyper-heuristic is to find and assemble good optimisation heuristics. Different operations or techniques can be introduced as heuristics so the overall optimisation could be more effective and more efficient.

Hyper-heuristic often begins from randomly generated initial solution and then iteratively improve the solution. A traditional selection hyper-heuristic approach has two key components: low level heuristics and high level strategy. The low level heuristics operate on the solution space. The quality of solution is being evaluated by the objective function from the domain. Whereas high level strategy operate on the heuristic space. It will form heuristics to improve the result and secondly it will also determine whether to accept or reject the generated solution by the acceptance criterion. The components of this framework are briefly described below:

4.1 High Level Strategy

The high level strategy uses the past search performance of low level heuristics to decide which heuristic should be applied at each decision point. It selects one from a pool of heuristics in the low level. This work uses the Multi-Armed Bandit (MAB) as an on-line heuristic selector [19, 20]. MAB is based on the record of past performance, e.g. the performance in previous iterations. The record stores an empirical reward and confidence level. The former is the average rewards achieved by that heuristic. The confidence level is the number of times that the heuristic has been selected. The higher values of these two scores indicate better quality of the heuristic [21]. MAB goes through all heuristics one by one and selects the one which returns the maximum value when applied Eq. (2).

$$\begin{aligned} \arg \max _{i=LLH_1 \dots LLH_n} \left( q_{i(t)}\,+\,c \sqrt{\frac{2log\sum _{i=LLH_1}^{LLH_n}n_{i(t)}}{n_{i(t)}}} \right) \end{aligned}$$
(2)

where \(LLH_n\) is the total number of heuristics in the low level, \(n_{i(t)}\) is number of times that \(i^{th}\) heuristic has been applied up to time t and \(q_{i(t)}\) is the empirical reward of the \(i^{th}\) heuristics up to time t which is calculated as follows: \(q_{i(t)}=q_{i(t)}\) + \(\varDelta \), where \(\varDelta \) is the difference between the quality of the old and new solutions.

4.2 Acceptance Criterion

Acceptance criterion is in the high level and is independent of the domain. Monte Carlo acceptance criterion is used in this study [15]. A solution that improve the objective function will be accepted if the following condition is met [21].

$$\begin{aligned} R < exp ( \varDelta f ) = exp ( f_t - f_{t-1} ) \end{aligned}$$
(3)

where R is the random number between [0, 1] and \(\varDelta f\) is the difference between performance at \((t-1)\)th and (t)th iterations.

4.3 Low Level Heuristics

In this work, 18 heuristics are included in the low level. Every heuristic has different characteristics hence may lead to different search behaviours. We use the following six heuristics to form the set of low level heuristics. Each heuristic is used in several ways to change one, two, three, real values parameters only, integer parameters only or all parameters.

Parametrised Gaussian Mutation

$$\begin{aligned} X_i = X_i + N(0, \sigma ^2) \end{aligned}$$
(4)

where \(\sigma ^2 \) is 0.5 times the standard deviation [21].

There another three operators which are the same as above but with different \( \sigma \) values ranged from 0.2, 0.3 and 0.4 of the standard deviation.

Differential Mutation

$$\begin{aligned} X_i = X_i + F \times (X_{1i} - X_{2i}) \forall i = 1...n \end{aligned}$$
(5)

where \(X_i\) is the decision variable for a given solution and \(X_1i\) is the best solution and F is the scaling factor [21].

Arithmetic Crossover

$$\begin{aligned} X_i = \lambda \times X_i + (1 - \lambda ) \times X_{1i}, \forall i = 1...N \end{aligned}$$
(6)

where \( \lambda \) is random number with range 0 to 1. \(X_i \) is the current solution and \(X_1i\) is the current best solution [21].

4.4 Initial Solution

This in our study is a set of CNN parameters that need to be tuned. These parameters are represented as an array. Each parameter initially is randomly generated. The random function is as follows:

$$\begin{aligned} x_p = l_p + Rand_p(0,1) \times (u_p - l_p), p=1...p \end{aligned}$$
(7)

where p is the total number of parameters to be tuned. \( Rand_p \) returns a random number within 0 and 1. \(l_p\) and \(u_p\) are lower bound and upper bound respectively for that parameter [21].

5 Experiments and Results

The first set of experiments are for image classifications. There are two most commonly used optimisers that were studied, namely Adam and Adadelta. In [22], it was mentioned that Adam and Adadelta provide the best convergence during the learning process. Table 1 show the classification performance on noisy MNIST sets with these two optimisers. The learning rate was set as 0.2 for all experiments. This preliminary experiments show that Adadelta can achieve better accuracy in comparison with Adam.

Table 1. Experiment with training on MNIST and testing on n-MNIST
Full size table

After a range of preliminary experiments, we settled on the settings include the optimisation algorithm, learning rate, drop out rate and number of neurons in the dense layer to start our experiment on classifying the noisy-MNIST and MNIST images. The images for training data are more than 60,000. We decrease the data size by half starting from \(2^{16} = 65540\) images to see the impact on test accuracy. For each size we repeat the experiment 30 times. The results are shown in Table 2 including the average training accuracies and test accuracies of the 30 runs. The epochs are all set as 10 to be consistent.

As we can see from Table 2, the classification performance between training on 65540 images and 512 images are not much different, meaning 512 is sufficient for training image classifiers to recognise good quality images. The drop in performance between 512 and 64 images is not major as well. The set of 32 images starts showing significant performance loss indicating more training images are required. When the training size is as small as 4, the test accuracy becomes 50% which is pretty much random guessing for this binary classification task.

Table 2. Experiment with different training sizes
Full size table
Table 3. Experiment with different training size using hyper-heuristic approach
Full size table

The above experiments confirm that the size of training dataset does impact on training. In the next set of experiments the hyper-heuristic approach presented in Sect. 4 is added in the learning process to tune the network parameters. The results are shown in Table 3 which listed the average test accuracies of 30 runs on training set of size 512 to that of size 4. Sizes above 512 are not included as the results from these sets would be all similar and close to 100%. For comparison purposes, the test results of training without the hyper-heuristic approach from Table 2 are repeated in the middle column of Table 3.

From test accuracies listed in Table 3 we can see the big improvement introduced by the hyper-heuristics approach on sizes 32 and 16. For larger size there are still performance increases but there are not much room for improvement. For smaller size like size 4, the sample is too few to be learnable hence the parameter tuning could not be much of help. This result indicates that with the hyper-heuristic tuning approach, it is possible to reduce the required training size. For applications of which training examples are few or expensive to obtain, our parameter optimisation could be very helpful.

To investigate the computational cost of the parameter optimisation, we also measured the running time of the above experiments which were all conducted on a machine with Intel core i3 with processor 1.90 GHz, 4.00 GB RAM and 64-bit Windows 10. The results are presented in Fig. 6 which shows the average time in seconds of 30 runs of learning on sizes 4, 8 up to 128, with and without the hyper-heuristic parameter optimisation. As can be seen on the figure, the optimisation process does take extra time. However the time increase is acceptable, maximum of a double time in the case of 128 training images. In comparison, exact methods for combinatorial optimisation are too expensive to be practical.

Fig. 6.
figure 6

Comparison on running time with and without hyper-heuristic optimization

Full size image
Fig. 7.
figure 7

Test accuracies with and without hyper-heuristic parameter optimisation

Full size image

From the above experiments we can see the hyper-heuristic approach can greatly improve learning without requiring too much extra computational resources. To further illustrate the differences realised by our hyper-heuristic approach, the test performance on different sizes are plotted as in Fig. 7. The lines represent the average of 30 runs, while the bars on size 4 to size 64 are the standard deviation of these 30 runs of using and without using hyper-heuristic optimisation. As can be seen in this figure, the gap at size 16 and at size 32 are significant. To verify the significance, T-tests are conducted on test accuracies on size 16 which resulted a p-value of 0.000002, and on size 32 which resulted a p-value of 0.000025. These p-values are way below the null hypothesis threshold 0.05, showing the differences that hyper-heuristic optimisation made on test performance are indeed significant.

6 Conclusions

In this work, we utilised deep learning to classify images of good quality versus images of poor quality without understanding or examining the image content. Based on our investigation using MNIST and n-MNIST benchmark, we can conclude that deep learning with convolutional neural networks can handle this type of image classification tasks and can achieve high performance with sufficient amount of training images. Our study also confirms that the learning performance is affected by training size. Learning image quality classifiers does not need large amount of samples. However the learning would still suffer if the training set is too small.

Another important part of this study is introducing hyper-heuristic approach based parameter optimisation to automatic configure the learning. Through our experiments it is clear that this optimisation method can improve the learning especially when the training size is not sufficient but not too few. Furthermore, the additional computational cost introduced by our hyper-heuristic method is not too expensive. That makes this method attractive especially in real world applications where training samples might be expensive or difficult to obtain.