Automated Measurement of Translational Margins and Rotational Shifts in Pelvic Structures Using CBCT Images of Rectal Cancer Patients

Abstract

Clinical radiotherapy procedures target to achieve high accuracy which is inhibited by various error sources. As a result, a safety margin is needed to ensure that the planned dosage is delivered to the target. In this work, 3D image coordinates of Pubic Symphysis (pb) and Coccyx are evaluated from Cone Beam CT images of colo-rectal cancer patients. Using those coordinates, we propose an automated method to obtain systematic and random error components. The standard deviations of systematic and random errors are used to evaluate the 3D PTV margin. We have also measured rotational variations in the positioning of patients using those locations. We have validated and found that the automated measurements show a very good match with those measured by oncologists manually.

1 Introduction

The procedures of clinical radiotherapy target to achieve high accuracy [1]. As treatment preparation involves various errors, a safety margin is required to ensure that the planned dose is actually delivered to the target. The margin calculations require reference bony structures because bones are good surrogates to detect internal motion of organs like rectum [1]. In [2], the authors evaluate the 3D locations of Pubic Symphysis (pb) and Coccyx. These are then used as reference structures in the pelvic region from Cone Beam Computed Tomography (CBCT) image volumes of colo-rectal cancer patients. On a day to day basis, there are considerable variations in the locations of pb and coccyx. The CBCT image volumes are, therefore, registered using Mean Shift assisted Mutual Information based 3D Registration (MSMIR) technique to reduce these uncertainties. In the report given by International Commission on Radiation Units and Measurements (ICRU) [3], it is mentioned that the volume that should receive the prescribed dose, is Clinical Target Volume (CTV), comprising of demonstrable tumor and/or areas of suspected subclinical disease. To account for the geometrical uncertainties, CTV must be expanded with a 3D margin thereby yielding Planning Target Volume (PTV).

In our study, the acquisition of CBCT images of a rectal cancer patients is carried out for a series of 27 days to obtain 27 CBCT image volumes. Only on the first day of the diagnosis, along with CBCT, a planning CT scan is also carried out with reference to which the shifts in the positions of pb and coccyx are evaluated. Usually, radiation treatment (RT) is given in multiple fractions of radiation to the evaluated PTV. When the total dose of radiation is divided into several, smaller doses over a period of several days, there are fewer toxic effects on healthy cells.

During a treatment regime, any deviation from planned irradiation geometry may be systematic or random. Systematic errors occur if the mean irradiation geometry in the fractionated treatment differs from the geometry in the treatment plan. The mean deviations of coordinates are then called systematic errors. Day-to-day differences around the mean deviation are called random errors [4]. Van Herk [1] proposed a model for deriving the PTV margin which is given as Margin = 2.5 $\varSigma$ + 0.7 $\sigma$. The criterion for this was that on an average, more than 99% of the CTV should get at least 95% of the dose. Mainly, our contributions in this work are as follows:

• 1. Automated computation of translational and rotational shifts, 3D PTV margins for colo-rectal cancer patients,

• 2. Higher accuracy in the computation of error margins, and

• 3. Use of conventional imaging procedure only, requiring no additional imaging or investigation procedure on the patients.

Conformal radiotherapy treatment on patients suffering from prostate cancer is done using infrared (IR) marker based positioning system over 553 treatment fractions [5]. Standard deviation of anteroposterior (AP) and lateral set up errors was considerably reduced to 4.8 mm compared to conventional technique. The main drawback is that IR system could not correctly locate markers which lead to execution failure in 21% of 553 fractions.

Using kilovoltage CBCT in combination with a diet and mild laxatives, work in [6] evaluated clinical results of adaptive radiotherapy protocol for prostate cancer. Compared to historical data which was without diet and laxatives, systematic and random errors for organ motion were reduced by a factor of 2. The laxatives, that were used, improved image quality, and thereby helped in detecting prostate reducing high dose region by 29%.

The work in [7] gives the effect of random and systematic deviations on target dose in the form of an analytical description. Higher random variations imply underdosage to CTV for a large number of patients, while the equal systematic error implies much larger underdosage for some of the patients. During the preparation stage of radiotherapy for prostate cancer, it reduces the uncertainty in the position of prostate and the shape of rectum. The motion of prostate relative to pelvic bone is quantified by matching CT scan with planning CT. The systematic error was $5.1^\circ$, and the random error was $3.6^\circ$.

2 Computation of Translational and Rotational Error Margins

In this work, we consider the first day 3D image coordinates of pb and coccyx as reference, to find out the shift in their positions for next 26 consecutive days. These shifts are considered to evaluate the systematic and random errors. The shifts in the positions are represented by a vector $\varvec{E}_{B_{ij}}$ for the $i^{th}$ patient on the $j^{th}$ day, where B $\in [\textit{pb}, \textit{coccyx}]$. In this work, a vector is represented by a bold and italicized alphabet like $\varvec{E}$.

$$\begin{aligned} \varvec{E}_{B_{ij}} = [(X_{ij} - X_{i1}),(Y_{ij} - Y_{i1}),(Z_{ij} - Z_{i1})], \forall i \in [1,P]\text { and } \forall j \in [1,N] \end{aligned}$$

where P is the number of patients under study, and N is the number of days of diagnosis. In our study, the values of P and N are 25 and 27, respectively. The vector $\varvec{E}$ is averaged for pb and coccyx to find shift in entire patient volume which is represented as $\varvec{E}_{a_{ij}}$, where subscript a denotes the averaging operation.

The 3D mean of the shifts for N days is represented by $\varvec{M}_{a_{i}}$ for a particular (the $i^{th}$) patient.

$$\begin{aligned} \varvec{M}_{a_{i}} = (\frac{\sum _{j=1}^{N} (X_{ij} - X_{i1})}{N}, \frac{\sum _{j=1}^{N} (Y_{ij} - Y_{i1})}{N}, \frac{\sum _{j=1}^{N} (Z_{ij} - Z_{i1})}{N}), \forall i \in [1,P] \end{aligned}$$

The 3D standard deviations of the shifts for daily measurements are represented by $\varvec{S}_{a_{i}}$ for a particular (the $i^{th}$) patient. We represent unit vectors in the directions of X, Y and Z by $\hat{x}$, $\hat{y}$ and $\hat{z}$ respectively. Dot product of any vector with $\hat{x}$, $\hat{y}$ and $\hat{z}$ gives out only the x, y and z components, respectively.

$$\begin{aligned} \varvec{S}_{a_{i}} = (\sqrt{\frac{\sum _{j=1}^{N} (\varvec{E}_{a_{ij}}.\hat{x} - \varvec{M}_{a_{i}}.\hat{x})^2}{N}}, \sqrt{\frac{\sum _{j=1}^{N} (\varvec{E}_{a_{ij}}.\hat{y} - \varvec{M}_{a_{i}}.\hat{y})^2}{N}}, \sqrt{\frac{\sum _{j=1}^{N} (\varvec{E}_{a_{ij}}.\hat{z} - \varvec{M}_{a_{i}}.\hat{z})^2}{N}}), \forall i \in [1,P] \end{aligned}$$

Then the Group Systematic Error (GSE), which is the mean evaluated over the entire group of patients is represented by a vector $\varvec{G}_{a}$.

$$\begin{aligned} \varvec{G}_{a} = (\frac{\sum _{i=1}^{P} \varvec{M}_{a_{i}}.\hat{x}}{P}, \frac{\sum _{i=1}^{P} \varvec{M}_{a_{i}}.\hat{y}}{P}, \frac{\sum _{i=1}^{P} \varvec{M}_{a_{i}}.\hat{z}}{P}) \end{aligned}$$

The standard deviations of the systematic errors is represented by a vector $\varvec{\varSigma }_{a}$.

$$\begin{aligned} \varvec{\varSigma }_{a} = (\sqrt{\frac{\sum _{i=1}^{P} (\varvec{M}_{a_{i}}.\hat{x} - \varvec{G}_{a_{i}}.\hat{x})^2}{P}}, \sqrt{\frac{\sum _{i=1}^{P} (\varvec{M}_{a_{i}}.\hat{y} - \varvec{G}_{a_{i}}.\hat{y})^2}{P}}, \sqrt{\frac{\sum _{i=1}^{P} (\varvec{M}_{a_{i}}.\hat{z} - \varvec{G}_{a_{i}}.\hat{z})^2}{P}}) \end{aligned}$$

And the standard deviations of the random errors are the root mean square of all the standard deviations of all the patients represented by a vector $\varvec{\sigma }_{a}$.

$$\begin{aligned} \varvec{\sigma }_{a} = (\sqrt{\frac{\sum _{i=1}^{P} (\varvec{S}_{a_{i}}.\hat{x})^2}{P}}, \sqrt{\frac{\sum _{i=1}^{P} (\varvec{S}_{a_{i}}.\hat{y})^2}{P}}, \sqrt{\frac{\sum _{i=1}^{P} (\varvec{S}_{a_{i}}.\hat{z})^2}{P}}) \end{aligned}$$

Fig. 1.

Demonstration of the calculations of Pitch and Yaw.

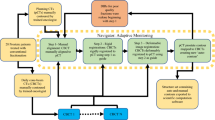
On a day-to-day basis, along with translational variations, there occur rotational variations in the position of patients. Before RT, to prepare treatment planning, the positioning of the patient has to be corrected in terms of rotations made in all the three axes. In this work, we have considered the first day 3D axis joining pb and coccyx as the reference to find rotational variations for the next 26 consecutive days. The sequence of steps to do this are:

• 1. We translate 3D coccyx coordinates of second day to that of the first day.

• 2. Then we project the 3D axes (defined by pb and coccyx) of two days onto the XY plane.

• 3. The angles made by the 3D axes with their projected 2D axes are denoted by $\theta 1$ and $\theta 2$, respectively, whose difference is referred to Pitch ($\theta$) in Fig. 1.

• 4. The angle between the projected 2D axes is referred to Yaw ($\phi$) in Fig. 1.

3 Results

The box plots showing variation of different measurements are shown in Fig. 2. The Euclidean norm of vectors $\varvec{M}$ and $\varvec{S}$ provide average shifts in locations of pb and coccyx. We observe that the means (horizontal line) in first two boxes (automated and manual-translational) of a patient are close to each other validating the computational process. The two ends or whiskers of those two boxes show that their distributions are also similar. The third box of each patient gives the Euclidean norm of rotational variations which are relatively constant for all the patients. We observe that smaller rotational values indicate the better adherence to the fractionated RT for a patient [8]. The observations done till now in prior works were all about tracking the motion of a particular organ. But, in this work, we provided a more generalised way of detecting shifts in the position of patients. As rectum stays relatively more stable with respect to pelvic bony structures (i.e. pb and coccyx in this case), the most suitable way of detecting the motion of rectum is to detect the motion of bones. Lesser the difference between $\varvec{\varSigma }$ and $\varvec{\sigma }$, lesser the underdosage to the target [7], as shown in Table 1. We observe that the difference between $\varvec{\varSigma }$ and $\varvec{\sigma }$ is small. As a result, it is expected that the underdosage to the PTV would be less probable during RT.

Fig. 2.

Variations in translational and rotational shifts for all the patients.

Table 1. PTV margins evaluated considering the standard deviations of random and systematic errors.

It can be observed that the vector $\varvec{G}$ in Table 1 deviating a little from zero which is expected because of imprecision in the equipment. It is found that the vectors $\varvec{G}$ and $\varvec{\varSigma }$ in z-direction are slightly higher which indicates a slight higher internal organ motion in that direction [8]. We also observe that the vectors $\varvec{G}$, $\varvec{\varSigma }$, $\varvec{\sigma }$ and 3D PTV margin calculated automatically are highly matching with those values evaluated manually. It shows that this automated system can be a very good replacement for manual efforts which aids oncologists in treatment planning before RT.

4 Conclusion

In this work, the 3D image coordinates of pb and coccyx are used to calculate the translational and rotational shifts. The average of shifts in the positions of pb and coccyx are considered to find variations in the position of the whole patient volume on day-to-day basis. These variations are used to obtain the 3D PTV margin using Van Herk [1] recipe for focusing prescribed radiation dose to the target. The first day 3D axis joining pb and coccyx is taken as reference to align 3D axes of remaining days with it. The 3D locations of pb and coccyx found in this work are more accurate than those found in [9]. We have validated our results with the measurements provided by an oncologist for the same set of patients as shown in Table 1. From Fig. 2, we observe that the rotational variations are quite small compared to those evaluated in [8]. This automated process of estimating the systematic, random errors, 3D PTV margin and rotations requires only the CBCT image volumes of the patients and does not need any other supportive data or expensive imaging technology. The proposed technique is fast, it involves no manual intervention, and reduces the occurrence of human errors.