Sublabel-Accurate Convex Relaxation of Vectorial Multilabel Energies

Abstract

Convex relaxations of multilabel problems have been demonstrated to produce provably optimal or near-optimal solutions to a variety of computer vision problems. Yet, they are of limited practical use as they require a fine discretization of the label space, entailing a huge demand in memory and runtime. In this work, we propose the first sublabel accurate convex relaxation for vectorial multilabel problems. Our key idea is to approximate the dataterm in a piecewise convex (rather than piecewise linear) manner. As a result we have a more faithful approximation of the original cost function that provides a meaningful interpretation for fractional solutions of the relaxed convex problem.

E. Laude and T. Möllenhoff—These authors contributed equally.

Technical University of Munich—This work was supported by the ERC Starting Grant “Convex Vision”.

1 Introduction

1.1 Nonconvex Vectorial Problems

In this paper, we derive a sublabel-accurate convex relaxation for vectorial optimization problems of the form

$$\begin{aligned} \underset{u : \varOmega \rightarrow \varGamma }{\min }~ \int _{\varOmega } \rho \big (x, u(x)\big ) \,\mathrm {d}x \,+\, \lambda \,TV(u), \end{aligned}$$

(1)

where $\varOmega \subset \mathbb {R}^d$, $\varGamma \subset \mathbb {R}^n$ and $\rho : \varOmega \times \varGamma \rightarrow \mathbb {R}$ denotes a generally nonconvex pointwise dataterm. As regularization we focus on the total variation defined as:

$$\begin{aligned} TV(u) = \underset{q \in C_c^{\infty }(\varOmega , \mathbb {R}^{n \times d}), \Vert q(x) \Vert _{S^{\infty }} \le 1}{\sup }~ \int _{\varOmega } \langle u,{\text {Div}}q\rangle ~ \mathrm {d}x, \end{aligned}$$

(2)

where $\Vert \cdot \Vert _{S^{\infty }}$ is the Schatten-$\infty$ norm on $\mathbb {R}^{n \times d}$, i.e., the largest singular value. For differentiable functions u we can integrate (2) by parts to find

$$\begin{aligned} TV(u) = \int _{\varOmega } \Vert \nabla u(x) \Vert _{S^1} ~ \mathrm {d}x, \end{aligned}$$

(3)

where the dual norm $\Vert \cdot \Vert _{S^1}$ penalizes the sum of the singular values of the Jacobian, which encourages the individual components of u to jump in the same direction. This type of regularization is part of the framework of Sapiro and Ringach [19].

1.2 Related Work

Due to its nonconvexity the optimization of (1) is challenging. For the scalar case ($n=1$), Ishikawa [9] proposed a pioneering technique to obtain globally optimal solutions in a spatially discrete setting, given by the minimum s-t-cut of a graph representing the space $\varOmega \times \varGamma$. A continuous formulation was introduced by Pock et al. [15] exhibiting several advantages such as less grid bias and parallelizability.

In a series of papers [14, 16], connections of the above approaches were made to the mathematical theory of cartesian currents [6] and the calibration method for the Mumford-Shah functional [1], leading to a generalization of the convex relaxation framework [15] to more general (in particular nonconvex) regularizers.

In the following, researchers have strived to generalize the concept of functional lifting and convex relaxation to the vectorial setting ($n > 1$). If the dataterm and the regularizer are both separable in the label dimension, one can simply apply the above convex relaxation approach in a channel-wise manner to each component separately. But when either the dataterm or the regularizer couple the label components, the situation becomes more complex [8, 20].

The approach which is most closely related to our work, and which we consider as a baseline method, is the one by Lellmann et al. [11]. They consider coupled dataterms with coupled total variation regularization of the form (2).

A drawback shared by all mentioned papers is that ultimately one has to discretize the label space. While Lellmann et al. [11] propose a sublabel-accurate regularizer, we show that their dataterm leads to solutions which still have a strong bias towards the label grid. For the scalar-valued setting, continuous label spaces have been considered in the MRF community by Zach and Kohli [22] and Fix and Agarwal [5]. The paper [21] proposes a method for mixed continuous and discrete vectorial label spaces, where everything is derived in the spatially discrete MRF setting. Möllenhoff et al. [12] recently proposed a novel formulation of the scalar-valued case which retains fully continuous label spaces even after discretization. The contribution of this work is to extend [12] to vectorial label spaces, thereby complementing [11] with a sublabel-accurate dataterm.

1.3 Contribution

In this work we propose the first sublabel-accurate convex formulation of vectorial labeling problems. It generalizes the formulation for scalar-valued labeling problems [12] and thus includes important applications such as optical flow estimation or color image denoising. We show that our method, derived in a spatially continuous setting, has a variety of interesting theoretical properties as well as practical advantages over the existing labeling approaches:

• We generalize existing functional lifting approaches (see Sect. 2.2).

• We show that our method is the best convex under-approximation (in a local sense), see Propositions 1 and 2.

• Due to its sublabel-accuracy our method requires only a small amount of labels to produce good results which leads to a drastic reduction in memory. We believe that this is a vital step towards the real-time capability of lifting and convex relaxation methods. Moreover, our method eliminates the label bias, that previous lifting methods suffer from, even for many labels.

• In Sect. 2.3 we propose a regularizer that couples the different label components by enforcing a joint jump normal. This is in contrast to [8], where the components are regularized separately.

• For convex dataterms, our method is equivalent to the unlifted problem – see Proposition 4. Therefore, it allows a seamless transition between direct optimization and convex relaxation approaches.

1.4 Notation

We write $\langle x,y\rangle = \sum _i x_i y_i$ for the standard inner product on $\mathbb {R}^n$ or the Frobenius product if x, y are matrices. Similarly $\Vert \cdot \Vert$ without any subscript denotes the usual Euclidean norm, respectively the Frobenius norm for matrices.

We denote the convex conjugate of a function $f : \mathbb {R}^n \rightarrow \mathbb {R}\cup \{ \infty \}$ by $f^*(y) = \sup _{x \in \mathbb {R}^n} ~ \langle y,x\rangle - f(x)$. It is an important tool for devising convex relaxations, as the biconjugate $f^{**}$ is the largest lower-semicontinuous (lsc.) convex function below f. For the indicator function of a set C we write $\delta _C$, i.e., $\delta _C(x) = 0$ if $x \in C$ and $\infty$ otherwise. $\varDelta _n^U \subset \mathbb {R}^n$ stands for the unit n-simplex.

2 Convex Formulation

2.1 Lifted Representation

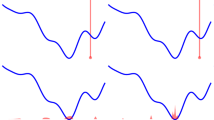
Motivated by Fig. 1, we construct an equivalent representation of (1) in a higher dimensional space, before taking the convex envelope.

Let $\varGamma \subset \mathbb {R}^n$ be a compact and convex set. We partition $\varGamma$ into a set $\mathcal {T}$ of n-simplices $\varDelta _i$ so that $\varGamma$ is a disjoint union of $\varDelta _i$ up to a set of measure zero. Let $t^{i_j}$ be the j-th vertex of $\varDelta _i$ and denote by $\mathcal {V}= \{t^1,\ldots ,t^{\left| {\mathcal {V}}\right| }\}$ the union of all vertices, referred to as labels, with $1\le i \le \left| {\mathcal {T}}\right|$, $1 \le j \le n+1$ and $1 \le i_j \le \left| {\mathcal {V}}\right|$. For $u : \varOmega \rightarrow \varGamma$, we refer to u(x) as a sublabel. Any sublabel can be written as a convex combination of the vertices of a simplex $\varDelta _i$ with $1\le i \le \left| {\mathcal {T}}\right|$ for appropriate barycentric coordinates $\alpha \in \varDelta _n^U$:

$$\begin{aligned} u(x)=T_i \alpha := \sum _{j=1}^{n+1}\alpha _j t^{i_j}, ~ T_i:=(t^{i_1},\ t^{i_2},\ \dots , \ t^{i_{n+1}}) \in \mathbb {R}^{n \times n+1}. \end{aligned}$$

(4)

By encoding the vertices $t^k \in \mathcal {V}$ using a one-of-$\left| {\mathcal {V}}\right|$ representation $e^k$ we can identify any $u(x) \in \varGamma$ with a sparse vector $\varvec{u}(x)$ containing at least $\left| {\mathcal {V}}\right| -n$ many zeros and vice versa:

$$\begin{aligned} \begin{aligned} \varvec{u}(x)&=E_i \alpha :=\sum _{j=1}^{n+1}\alpha _j e^{i_j}, ~ E_i:=(e^{i_1}, \ e^{i_2}, \dots , \ e^{i_{n+1}}) \in \mathbb {R}^{\left| {\mathcal {V}}\right| \times n+1}, \\ u(x)&= \sum _{k=1}^{\left| {\mathcal {V}}\right| } t^k \varvec{u}_k(x), ~ \alpha \in \varDelta _n^U, ~ 1\le i \le \left| {\mathcal {T}}\right| . \end{aligned} \end{aligned}$$

(5)

The entries of the vector $e^{i_j}$ are zero except for the $(i_j)$-th entry, which is equal to one. We refer to $\varvec{u}: \varOmega \rightarrow \mathbb {R}^{\left| {\mathcal {V}}\right| }$ as the lifted representation of u. This one-to-one-correspondence between $u(x) = T_i \alpha$ and $\varvec{u}(x) = E_i \alpha$ is shown in Fig. 2. Note that both, $\alpha$ and i depend on x. However, for notational convenience we drop the dependence on x whenever we consider a fixed point $x \in \varOmega$.

Fig. 1.

In (a) we show a nonconvex dataterm. Convexification without lifting would result in the energy (b). Classical lifting methods [11] (c), approximate the energy piecewise linearly between the labels, whereas the proposed method results in an approximation that is convex on each triangle (d). Therefore, we are able to capture the structure of the nonconvex energy much more accurately.

Fig. 2.

This figure illustrates our notation and the one-to-one correspondence between $u(x)=(0.3,0.2)^\top$ and the lifted $\varvec{u}(x)$ containing the barycentric coordinates $\alpha =(0.7,0.1,0.2)^\top$ of the sublabel $u(x)\in$ $\,=\,\mathrm {conv}\{t^2, t^3, t^6\}$. The triangulation $(\mathcal {V}, \mathcal {T})$ of $\varGamma =[-1;1]\times [0;1]$ is visualized via the gray lines, corresponding to the triangles and the gray dots, corresponding to the vertices $\mathcal {V} = \{(-1,0)^\top , (0,0)^\top , \dots , (1,1)^\top \}$, that we refer to as the labels.

2.2 Convexifying the Dataterm

Let for now the weight of the regularizer in (1) be zero. Then, at each point $x \in \varOmega$ we minimize a generally nonconvex energy over a compact set $\varGamma \subset \mathbb {R}^n$:

$$\begin{aligned} \underset{u \in \varGamma }{\min }~ \rho (u). \end{aligned}$$

(6)

We set up the lifted energy so that it attains finite values if and only if the argument $\varvec{u}$ is a sparse representation $\varvec{u}= E_i \alpha$ of a sublabel $u \in \varGamma$:

$$\begin{aligned} \varvec{\rho }(\varvec{u}) = \min _{1\le i \le \left| {\mathcal {T}}\right| } ~ \varvec{\rho }_i(\varvec{u}), \qquad \varvec{\rho }_i(\varvec{u}) = {\left\{ \begin{array}{ll} \rho (T_i \alpha ), \qquad &{}\text {if } ~ \varvec{u}= E_i \alpha , ~ \alpha \in \varDelta _n^U,\\ \infty , &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(7)

Problems (6) and (7) are equivalent due to the one-to-one correspondence of $u=T_i \alpha$ and $\varvec{u}= E_i \alpha$. However, energy (7) is finite on a nonconvex set only. In order to make optimization tractable, we minimize its convex envelope.

Proposition 1

The convex envelope of (7) is given as:

$$\begin{aligned} \begin{aligned} \varvec{\rho }^{**}(\varvec{u})&= \sup _{\varvec{v} \in \mathbb {R}^{\left| {\mathcal {V}}\right| }} \langle \varvec{u}, \varvec{v}\rangle - \max _{1 \le i \le \left| {\mathcal {T}}\right| } ~ \varvec{\rho }_i^*(\varvec{v}), \\ \varvec{\rho }_i^*(\varvec{v})&= \langle E_i b_i, \varvec{v} \rangle + \rho _i^*(A_i^\top E_i^\top \varvec{v}), \quad \rho _i := \rho + \delta _{\varDelta _i}. \end{aligned} \end{aligned}$$

(8)

$b_i$ and $A_i$ are given as $b_i := M_i^{n+1}$, $A_i := \left( M_i^1, ~ M_i^2,~ \dots ,~ M_i^n \right)$, where $M_i^j$ are the columns of the matrix $M_i:=(T_i^\top , \mathbf {1})^{-\top } \in \mathbb {R}^{{n+1} \times {n+1}}$.

Proof

Follows from a calculation starting at the definition of $\varvec{\rho }^{**}$. See supplementary material for a detailed derivation.

Fig. 3.

Geometrical intuition for the proposed lifting and standard lifting [11] for the special case of 1-dimensional range $\varGamma =[a,b]$ and 3 labels $\{t^1,t^2,t^3\}$. The standard lifting correponds to a linear interpolation of the original cost in between the locations $t^1,t^2,t^3$, which are associated with the vertices $e^1,e^2,e^3$ in the lifted energy (lower left). The proposed method extends the cost to the relaxed set in a more precise way: The original cost is preserved on the connecting lines between adjacent $e^i$ (black lines on the bottom right) up to concave parts (red graphs and lower surface on the right). This information, which may influence the exact location of the minimizer, is lost in the standard formulation. If the solution of the lifted formulation $\varvec{u}$ is in the interior (gray area) an approximate solution to the original problem can still be obtained via Eq. (5). (Color figure online)

The geometric intuition of this construction is depicted in Fig. 3. Note that if one prescribes the value of $\varvec{\rho }_i$ in (7) only on the vertices of the unit simplices $\varDelta _n^U$, i.e., $\varvec{\rho }(\varvec{u})=\rho (t^k)$ if $\varvec{u}=e^k$ and $+\infty$ otherwise, one obtains the linear biconjugate $\varvec{\rho }^{**}(\varvec{u}) = \langle \varvec{u}, \varvec{s} \rangle ,\; \varvec{s} = (\rho (t^i),\ldots ,\rho (t^L))$ on the feasible set. This coincides with the standard relaxation of the dataterm used in [4, 10, 11, 16]. In that sense, our approach can be seen as a relaxing the dataterm in a more precise way, by incorporating the true value of $\rho$ not only on the finite set of labels $\mathcal {V}$, but also everywhere in between, i.e., on every sublabel.

2.3 Lifting the Vectorial Total Variation

We define the lifted vectorial total variation as

$$\begin{aligned} \varvec{TV}(\varvec{u}) = \int _{\varOmega } \varvec{\varPsi }(D \varvec{u}), \end{aligned}$$

(9)

where $D\varvec{u}$ denotes the distributional derivative of $\varvec{u}$ and $\varvec{\varPsi }$ is positively one-homogeneous, i.e., $\varvec{\varPsi }(c \varvec{u}) = c\, \varvec{\varPsi }(\varvec{u}), c \geqslant 0$. For such functions, the meaning of (9) can be made fully precise using the polar decomposition of the Radon measure $D \varvec{u}$ [2, Corollary 1.29, Theorem 2.38]. However, in the following we restrict ourselves to an intuitive motivation for the derivation of $\varvec{\varPsi }$ for smooth functions.

Our goal is to find $\varvec{\varPsi }$ so that $\varvec{TV}(\varvec{u}) = {TV}(u)$ whenever $\varvec{u}:\varOmega \rightarrow \mathbb {R}^{\left| {\mathcal {V}}\right| }$ corresponds to some $u:\varOmega \rightarrow \varGamma$, in the sense that $\varvec{u}(x) = E_i \alpha$ whenever $u(x) = T_i \alpha$. In order for the equality to hold, it must in particular hold for all u that are classically differentiable, i.e., $D u = \nabla u$, and whose Jacobian $\nabla u(x)$ is of rank 1, i.e., $\nabla u(x) = (T_i \alpha - T_j \beta ) \otimes \nu (x)$ for some $\nu (x) \in \mathbb {R}^d$. This rank 1 constraint enforces the different components of u to have the same jump normal, which is desirable in many applications. In that case, we observe

$$\begin{aligned} TV(u) = \int _\varOmega \Vert T_{i} \alpha - T_{j} \beta \Vert \cdot \Vert \nu (x)\Vert \, \mathrm {d} x. \end{aligned}$$

(10)

For the corresponding lifted representation $\varvec{u}$, we have $\nabla \varvec{u}(x) = (E_i \alpha - E_j \beta ) \otimes \nu (x)$. Therefore it is natural to require $\varvec{\varPsi }(\nabla \varvec{u}(x)) = \varvec{\varPsi }\left( (E_i \alpha - E_j \beta ) \otimes \nu (x) \right) := \Vert T_i \alpha -T_j \beta \Vert \cdot \Vert \nu (x)\Vert$ in order to achieve the goal $\varvec{TV}(\varvec{u}) = {TV}(u)$. Motivated by these observations, we define

$$\begin{aligned} \varvec{\varPsi }(\varvec{p}):={\left\{ \begin{array}{ll} \Vert T_i \alpha - T_j \beta \Vert \cdot \Vert \nu \Vert &{} \text {if } ~ \varvec{p}=(E_i \alpha - E_j \beta )\otimes \nu , \\ \infty &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(11)

where $\alpha , \beta \in \varDelta _{n+1}^U$, $\nu \in \mathbb {R}^d$ and $1 \le i,j \le \left| {\mathcal {T}}\right|$. Since the convex envelope of (9) is intractable, we derive a “locally” tight convex underapproximation:

$$\begin{aligned} \varvec{R}(\varvec{u}) = \sup _{\varvec{q}: \varOmega \rightarrow \mathbb {R}^{d \times \left| {\mathcal {V}}\right| }} \int _{\varOmega } \langle \varvec{u},{\text {Div}}\varvec{q}\rangle - \varvec{\varPsi }^*(\varvec{q}) \ \mathrm {d}x. \end{aligned}$$

(12)

Proposition 2

The convex conjugate of $\varvec{\varPsi }$ is

$$\begin{aligned} \varvec{\varPsi }^*(\varvec{q})=\delta _\mathcal {K}(\varvec{q}) \end{aligned}$$

(13)

with convex set

$$\begin{aligned} \mathcal {K}&=\bigcap _{1\le i,j \le \left| {\mathcal {T}}\right| } \left\{ \varvec{q} \in \mathbb {R}^{d \times \left| {\mathcal {V}}\right| } \bigm | \Vert Q_i \alpha - Q_j \beta \Vert \le \Vert T_i \alpha - T_j \beta \Vert , \ \alpha , \beta \in \varDelta _{n+1}^U \right\} , \end{aligned}$$

(14)

and $Q_i = (\varvec{q}^{i_1},\ \varvec{q}^{i_2}, \ \dots , \ \varvec{q}^{i_{n+1}}) \in \mathbb {R}^{d \times n+1}$. $\varvec{q}^j \in \mathbb {R}^d$ are the columns of $\varvec{q}$.

Proof

Follows from a calculation starting at the definition of the convex conjugate $\varvec{\varPsi }^*$. See supplementary material.

Interestingly, although in its original formulation (14) the set $\mathcal {K}$ has infinitely many constraints, one can equivalently represent $\mathcal {K}$ by finitely many.

Proposition 3

The set $\mathcal {K}$ in Eq. (14) is the same as

$$\begin{aligned} \mathcal {K}=\left\{ \varvec{q}\in \mathbb {R}^{d \times \left| {\mathcal {V}}\right| } \mid \left\| D_{\varvec{q}}^i \right\| _{S^\infty }\le 1, \ 1\le i\le \left| {\mathcal {T}}\right| \right\} , ~ D_{\varvec{q}}^i = Q_iD\,(T_iD)^{-1}, \end{aligned}$$

(15)

where the matrices $Q_iD \in \mathbb {R}^{d \times n}$ and $T_iD \in \mathbb {R}^{n \times n}$ are given as

$$\begin{aligned} Q_iD := \left( \varvec{q}^{i_1} - \varvec{q}^{i_{n+1}}, ~ \dots , ~\varvec{q}^{i_n} - \varvec{q}^{i_{n+1}}\right) , ~ T_iD:=\left( t^{i_1} - t^{i_{n+1}}, ~ \dots , ~t^{i_n} - t^{i_{n+1}}\right) . \end{aligned}$$

Proof

Similar to the analysis in [11], Eq. (14) basically states the Lipschitz continuity of a piecewise linear function defined by the matrices $\varvec{q}\in \mathbb {R}^{d \times \left| {\mathcal {V}}\right| }$. Therefore, one can expect that the Lipschitz constraint is equivalent to a bound on the derivative. For the complete proof, see supplementary material.

2.4 Lifting the Overall Optimization Problem

Combining dataterm and regularizer, the overall optimization problem is given

$$\begin{aligned} \min _{\varvec{u}: \varOmega \rightarrow \mathbb {R}^{\left| {\mathcal {V}}\right| }} \sup _{\varvec{q}: \varOmega \rightarrow \mathcal {K}} \int _{\varOmega } \varvec{\rho }^{**}(\varvec{u}) + \langle \varvec{u},{\text {Div}}\varvec{q}\rangle \ \mathrm {d}x. \end{aligned}$$

(16)

A highly desirable property is that, opposed to any other vectorial lifting approach from the literature, our method with just one simplex applied to a convex problem yields the same solution as the unlifted problem.

Proposition 4

If the triangulation contains only 1 simplex, $\mathcal {T} = \{ \varDelta \}$, i.e., $\left| {\mathcal {V}}\right| = n + 1$, then the proposed optimization problem (16) is equivalent to

$$\begin{aligned} \underset{u : \varOmega \rightarrow \varDelta }{\min }~ \int _{\varOmega } (\rho + \delta _\varDelta )^{**}(x, u(x)) \ \mathrm {d}x + \lambda TV(u), \end{aligned}$$

(17)

which is (1) with a globally convexified dataterm on $\varDelta$.

Proof

For $u = t^{n+1} + TD \tilde{u}$ the substitution $\varvec{u}= \left( \tilde{u}_1, \ldots , \tilde{u}_n, 1 - \sum _{j=1}^n \tilde{u}_j \right)$ into $\varvec{\rho }^{**}$ and $\varvec{R}$ yields the result. For a complete proof, see supplementary material.

3 Numerical Optimization

3.1 Discretization

For now assume that $\varOmega \subset \mathbb {R}^d$ is a d-dimensional Cartesian grid and let ${\text {Div}}$ denote a finite-difference divergence operator with ${\text {Div}}\varvec{q} : \varOmega \rightarrow \mathbb {R}^{\left| {\mathcal {V}}\right| }$. Then the relaxed energy minimization problem becomes

$$\begin{aligned} \min _{\varvec{u}: \varOmega \rightarrow \mathbb {R}^{\left| {\mathcal {V}}\right| }}\max _{\varvec{q} : \varOmega \rightarrow \mathcal {K}} ~ \sum _{x \in \varOmega } \varvec{\rho }^{**}(x, \varvec{u}(x)) + \langle {\text {Div}}\varvec{q}, \varvec{u}\rangle . \end{aligned}$$

(18)

In order to get rid of the pointwise maximum over $\varvec{\rho }_i^*(\varvec{v})$ in Eq. (8), we introduce additional variables $w(x) \in \mathbb {R}$ and additional constraints $(\varvec{v}(x), w(x)) \in \mathcal {C}$, $x \in \varOmega$ so that w(x) attains the value of the pointwise maximum:

$$\begin{aligned} \min _{\varvec{u}: \varOmega \rightarrow \mathbb {R}^{\left| {\mathcal {V}}\right| }} \max _{\begin{array}{c} (\varvec{v}, w):\varOmega \rightarrow \mathcal {C}\\ \varvec{q} : \varOmega \rightarrow \mathcal {K} \end{array}} ~ \sum _{x \in \varOmega } \langle \varvec{u}(x), \varvec{v}(x) \rangle - w(x) + \langle {\text {Div}}\varvec{q}, \varvec{u}\rangle , \end{aligned}$$

(19)

where the set $\mathcal {C}$ is given as

$$\begin{aligned} \mathcal {C} = \bigcap _{1\le i \le \left| {\mathcal {T}}\right| } \mathcal {C}_i, \quad \mathcal {C}_i:=\left\{ (x, y) \in \mathbb {R}^{\left| {\mathcal {V}}\right| +1} \mid \varvec{\rho }_i^*(x) \le y \right\} . \end{aligned}$$

(20)

For numerical optimization we use a GPU-based implementation¹ of a first-order primal-dual method [14]. The algorithm requires the orthogonal projections of the dual variables onto the sets $\mathcal {C}$ respectively $\mathcal {K}$ in every iteration. However, the projection onto an epigraph of dimension $\left| {\mathcal {V}}\right| +1$ is difficult for large values of $\left| {\mathcal {V}}\right|$. We rewrite the constraints $(\varvec{v}(x), w(x)) \in \mathcal {C}_i$, $1\le i \le \left| {\mathcal {T}}\right|$, $x\in \varOmega$ as $(n+1)$-dimensional epigraph constraints introducing variables $r^i(x)\in \mathbb {R}^n$, $s_i(x)\in \mathbb {R}$:

$$\begin{aligned} \rho _i^*\left( r^i(x)\right) \le s_i(x), \quad r^i(x)=A_i^\top E_i^\top \, \varvec{v}(x), \quad s_i(x) = w(x) - \langle E_i b_i, \varvec{v}(x) \rangle . \end{aligned}$$

(21)

These equality constraints can be implemented using Lagrange multipliers. For the projection onto the set $\mathcal {K}$ we use an approach similar to [7, Fig. 7].

3.2 Epigraphical Projections

Computing the Euclidean projection onto the epigraph of $\rho _i^*$ is a central part of the numerical implementation of the presented method. However, for $n > 1$ this is nontrivial. Therefore we provide a detailed explanation of the projection methods used for different classes of $\rho _i$. We will consider quadratic, truncated quadratic and piecewise linear $\rho$.

Quadratic Case: Let $\rho$ be of the form $\rho (u)=\frac{a}{2} \, u^\top u + b^\top u + c$. A direct projection onto the epigraph of $\rho _i^*=(\rho + \delta _{\varDelta _i})^*$ for $n > 1$ is difficult. However, the epigraph can be decomposed into separate epigraphs for which it is easier to project onto: For proper, convex, lsc. functions f, g the epigraph of $(f+g)^*$ is the Minkowski sum of the epigraphs of $f^*$ and $g^*$ (cf. [17, Exercise 1.28, Theorem 11.23a]). This means that it suffices to compute the projections onto the epigraphs of a quadratic function $f^*=\rho ^*$ and a convex, piecewise linear function $g^*(v)=\max _{1 \le j \le n+1} \langle t^{i_j},v\rangle$ by rewriting constraint (21) as

$$\begin{aligned} \rho ^*(r_{f})\le s_{f},~ {\delta _{\varDelta _i}}^*(c_{g}) \le d_{g} ~ \text { s.t. } (r,s)=(r_{f},s_{f})+(c_{g},d_{g}). \end{aligned}$$

(22)

For the projection onto the epigraph of a n-dimensional quadratic function we use the method described in [20, Appendix B.2]. The projection onto a piecewise linear function is described in the last paragraph of this section.

Truncated Quadratic Case: Let $\rho$ be of the form $\rho (u)= \min \,\{\,\nu , ~ \frac{a}{2}\, u^\top u + b^\top u + c\,\}$ as it is the case for the nonconvex robust ROF with a truncated quadratic dataterm in Sect. 4.2. Again, a direct projection onto the epigraph of $\rho _i^*$ is difficult. However, a decomposition of the epigraph into simpler epigraphs is possible as the epigraph of $\min \{f, g\}^*$ is the intersection of the epigraphs of $f^*$ and $g^*$. Hence, one can separately project onto the epigraphs of $(\nu + \delta _{\varDelta _i})^*$ and $(\frac{a}{2}\, u^\top u + b^\top u + c + \delta _{\varDelta _i})^*$. Both of these projections can be handled using the methods from the other paragraphs.

Piecewise Linear Case: In case $\rho$ is piecewise linear on each $\varDelta _i$, i.e., $\rho$ attains finite values at a discrete set of sampled sublabels $\mathcal {V}_i \subset \varDelta _i$ and interpolates linearly between them, we have that

$$\begin{aligned} (\rho + \delta _{\varDelta _i})^*(v)=\max _{\tau \in \mathcal {V}_i} ~ \langle \tau ,v\rangle - \rho (\tau ). \end{aligned}$$

(23)

Again this is a convex, piecewise linear function. For the projection onto the epigraph of such a function, a quadratic program of the form

$$\begin{aligned} \min _{(x,y) \in \mathbb {R}^{n+1}} ~ \frac{1}{2}\Vert x-c\Vert ^2 + \frac{1}{2}\Vert y-d\Vert ^2 ~\text { s.t. } \langle \tau ,x\rangle - \rho (\tau ) \le y, \forall \tau \in \mathcal {V}_i \end{aligned}$$

(24)

needs to be solved. We implemented the primal active-set method described in [13, Algorithm 16.3], and found it solves the program in a few (usually 2–10) iterations for a moderate number of constraints.

Fig. 4.

ROF denoising of a vector-valued signal $f : [0, 1] \rightarrow [-1, 1]^2$, discretized on 50 points (shown in red). We compare the proposed approach (right) with two alternative techniques introduced in [11] (left and middle). The labels are visualized by the gray grid. While the naive (standard) multilabel approach from [11] (left) provides solutions that are constrained to the chosen set of labels, the sublabel accurate regularizer from [11] (middle) does allow sublabel solutions, yet – due to the dataterm bias – these still exhibit a strong preference for the grid points. In contrast, the proposed approach does not exhibit any visible grid bias providing fully sublabel-accurate solutions: With only 4 labels, the computed solutions (shown in blue) coincide with the “unlifted” problem (green) (Color figure online).

4 Experiments

4.1 Vectorial ROF Denoising

In order to validate experimentally, that our model is exact for convex dataterms, we evaluate it on the Rudin-Osher-Fatemi [18] (ROF) model with vectorial TV (2). In our model this corresponds to defining $\rho (x, u(x))= \frac{1}{2}\Vert u(x) - I(x)\Vert ^2$. As expected based on Proposition 4 the energy of the solution of the unlifted problem is equal to the energy of the projected solution of our method for $|\mathcal {V}|=4$ up to machine precision, as can be seen in Figs. 4 and 5. We point out, that the sole purpose of this experiment is a proof of concept as our method introduces an overhead and convex problems can be solved via direct optimization. It can be seen in Figs. 4 and 5, that the baseline method [11] has a strong label bias.

4.2 Denoising with Truncated Quadratic Dataterm

For images degraded with both, Gaussian and salt-and-pepper noise we define the dataterm as $\rho (x, u(x))= \min \,\left\{ \frac{1}{2}\Vert u(x) - I(x)\Vert ^2, \nu \right\}$. We solve the problem using the epigraph decomposition described in the second paragraph of Sect. 3.2. It can be seen, that increasing the number of labels $\left| {\mathcal {V}}\right|$ leads to lower energies and at the same time to a reduced effect of the TV. This occurs as we always compute a piecewise convex underapproximation of the original nonconvex dataterm, that gets tighter with a growing number of labels. The baseline method [11] again produces strong discretization artefacts even for a large number of labels $\left| {\mathcal {V}}\right| =4\times 4\times 4=64$.

Fig. 5.

Convex ROF with vectorial TV. Direct optimization and proposed method yield the same result. In contrast to the baseline method [11] the proposed approach has no discretization artefacts and yields a lower energy. The regularization parameter is chosen as $\lambda =0.3$.

Fig. 6.

ROF with a truncated quadratic dataterm ($\lambda =0.03$ and $\nu =0.025$). Compared to the baseline method [11] the proposed approach yields much better results, already with a very small number of 4 labels.

Fig. 7.

We compute the optical flow using our method, the product space approach [8] and the baseline method [11] for a varying amount of labels and compare the average endpoint error (aep). The product space method clearly outperforms the baseline, but our approach finds the overall best result already with $2 \times 2$ labels. To achieve a similarly precise result as the product space method, we require 150 times fewer labels, 10 times less memory and 3 times less time. For the same number of labels, the proposed approach requires more memory as it has to store a convex approximation of the energy instead of a linear one.

4.3 Optical Flow

We compute the optical flow $v:\varOmega \rightarrow \mathbb {R}^2$ between two input images $I_1, I_2$. The label space $\varGamma = [-d, d]^2$ is chosen according to the estimated maximum displacement $d \in \mathbb {R}$ between the images. The dataterm is $\rho (x, v(x)) = \Vert I_2(x) - I_1(x + v(x)) \Vert$, and $\lambda (x)$ is based on the norm of the image gradient $\nabla I_1(x)$.

Fig. 8.

Large displacement flow between two $640\times 480$ images (a) using a $81 \times 81$ search window. The result of our method with 4 labels is shown in (b), the baseline [11] in (c). Our method can correctly identify the large motion.

In Fig. 7 we compare the proposed method to the product space approach [8]. Note that we implemented the product space dataterm using Lagrange multipliers, also referred to as the global approach in [8]. While this increases the memory consumption, it comes with lower computation time and guaranteed convergence. For our method, we sample the label space $\varGamma = [-15, 15]^2$ on $150 \times 150$ sublabels and subsequently convexify the energy on each triangle using the quickhull algorithm [3]. For the product space approach we sample the label space at equidistant labels, from $5 \times 5$ to $27 \times 27$. As the regularizer from the product space approach is different from the proposed one, we chose $\mu$ differently for each method. For the proposed method, we set $\mu = 0.5$ and for the product space and baseline approach $\mu = 3$. We can see in Fig. 7, our method outperforms the product space approach w.r.t. the average end-point error. Our method outperforms previous lifting approaches: In Fig. 8 we compare our method on large displacement optical flow to the baseline [11]. To obtain competitive results on the Middlebury benchmark, one would need to engineer a better dataterm.

5 Conclusions

We proposed the first sublabel-accurate convex relaxation of vectorial multilabel problems. To this end, we approximate the generally nonconvex dataterm in a piecewise convex manner as opposed to the piecewise linear approximation done in the traditional functional lifting approaches. This assures a more faithful approximation of the original cost function and provides a meaningful interpretation for the non-integral solutions of the relaxed convex problem. In experimental validations on large-displacement optical flow estimation and color image denoising, we show that the computed solutions have superior quality to the traditional convex relaxation methods while requiring substantially less memory and runtime.