Localized Verlet Integration Framework for Facial Models

Abstract

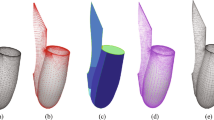
Traditional Verlet integration frameworks have been successful with their robustness and efficiency to simulate deformable bodies ranging from simple cloth to geometrically complex solids. However, the existing frameworks deform the models as a whole. We present a Verlet integration framework which provides local surface deformation on the selected area of the mesh without giving any global deformation impact to the whole model. The framework is specifically designed for facial surfaces of the cartoon characters in computer animation. Our framework provides an interactive selection of the deformation influence area by using geodesic distance computation based on heat kernel. Additionally, the framework exploits the geometric constraints for stretching, shearing and bending to handle the environmental interactions such as collision. The proposed framework is robust and easy to implement since it is based on highly accurate geodesic distance computation and solving the projected geometric constraints. We demonstrate the benefits of our framework with the results obtained from various facial models to present its potential in terms of practicability and effectiveness.

Appendix: Constraint Derivations

The constraint function for stretching from Eq. 8 is $C_1(q_{i,j}) = |D| - l_{ij}$ where $D = |q_j - q_i|$. The corresponding gradients are $\nabla _{q_i} C = -n$ and $\nabla _{q_j} C = n$ where $n = \frac{q_j - q_i}{|q_j - q_i|}$. After substituting the gradients to Eq. 7, the Lagrange multiplier becomes $\lambda = \frac{|q_j - q_i|-l}{|w_j + w_i|}$ where $w_i = w_j = 1$, and from [15] the final corrections are:

$$\begin{aligned} \varDelta q_i = -\frac{1}{2}(|q_j - q_i|-l)(\frac{q_j - q_i}{|q_j - q_i|}) \end{aligned}$$

(14)

$$\begin{aligned} \varDelta q_j = +\frac{1}{2}(|q_j - q_i|-l)(\frac{q_j - q_i}{|q_j - q_i|}) \end{aligned}$$

(15)

The constraint function for shearing from Eq. 9 is defined as $C(q_{i,j,k}) = cos^{-1}(D) - \gamma _{ijk}$, where $D = M_{ij} \cdot M_{ik}$ from Eq. 11. With $\frac{d}{dx} cos^{-1}(x) = -\frac{1}{\sqrt{1-x^2}}$, the corresponding gradients are obtained as follows:

$$\begin{aligned} \nabla _{q_i} C = -\frac{1}{\sqrt{1-D^2}} (\frac{\partial M_{ij}}{\partial q_i} \cdot M_{ik} + M_{ij} \cdot \frac{\partial M_{ik}}{\partial q_i}) \end{aligned}$$

(16)

$$\begin{aligned} \nabla _{q_j} C = -\frac{1}{\sqrt{1-D^2}} (\frac{\partial M_{ij}}{\partial q_j} \cdot M_{ik} + M_{ij} \cdot \frac{\partial M_{ik}}{\partial q_j}) \end{aligned}$$

(17)

$$\begin{aligned} \nabla _{q_k} C = -\frac{1}{\sqrt{1-D^2}} (\frac{\partial M_{ij}}{\partial q_k} \cdot M_{ik} + M_{ij} \cdot \frac{\partial M_{ik}}{\partial q_k}) \end{aligned}$$

(18)

After substituting the gradients to Eq. 7, the Lagrange multiplier becomes:

$$\begin{aligned} \lambda = -\frac{cos^{-1}(M_{ij} \cdot M_{ik}) - \gamma _{ijk}}{|\nabla _{q_i} C|^2 + |\nabla _{q_j} C|^2 + |\nabla _{q_k} C|^2} \end{aligned}$$

(19)

where $w_i = w_j = w_k = 1$. The corrections can be computed easily for the shearing constraint by substituting the gradients and Lagrange multiplier in Eq. 6. We use a middle step to demonstrate the calculations:

The general final correction for shearing constraint is:

$$\begin{aligned} \varDelta q_{i,j,k} = -\frac{(\sqrt{1-D^2})(cos^{-1}(D) - \gamma _{ijk})}{|r_1|^2 + |r_2|^2 + |r_3|^2} r_{1,2,3} \end{aligned}$$

(20)

The constraint function for bending from Eq. 10 is defined as $C(q_{i,j,k,l}) = cos^{-1}(D) - \theta _{ijkl}$, where $D = N_{ijk} \cdot N_{ijl}$ from Eq. 12. According to [15] $q_i$ is set to 0 ($q_i = 0$), with $\frac{d}{dx} cos^{-1}(x) = -\frac{1}{\sqrt{1-x^2}}$, the corresponding gradients are obtained as follows:

$$\begin{aligned} \nabla _{q_i} C = -\nabla _{q_j} C - \nabla _{q_k} C - \nabla _{q_l} C \end{aligned}$$

(21)

$$\begin{aligned} \nabla _{q_j} C = -\frac{1}{\sqrt{1-D^2}} ((\frac{\partial N_{ijk}}{\partial q_j})^T N_{ijl} + (\frac{\partial N_{ijl}}{\partial q_j})^T N_{ijk}) \end{aligned}$$

(22)

$$\begin{aligned} \nabla _{q_k} C = -\frac{1}{\sqrt{1-D^2}} ((\frac{\partial N_{ijk}}{\partial q_k})^T N_{ijl}) \end{aligned}$$

(23)

$$\begin{aligned} \nabla _{q_l} C = -\frac{1}{\sqrt{1-D^2}} ((\frac{\partial N_{ijl}}{\partial q_l})^T N_{ijk}) \end{aligned}$$

(24)

After substituting the gradients to Eq. 7, the Lagrange multiplier becomes:

$$\begin{aligned} \lambda = -\frac{cos^{-1}(N_{ijk} \cdot N_{ijl}) - \theta _{ijkl}}{|\nabla _{q_i} C|^2 + |\nabla _{q_j} C|^2 + |\nabla _{q_k} C|^2 + |\nabla _{q_l} C|^2} \end{aligned}$$

(25)

where $w_i = w_j = w_k = w_l = 1$. By following the form mentioned in [15], as a middle step, we take advantage of the following computations before finding the final corrections:

$$\begin{aligned} r_1 = -r_2 - r_3 - r_4 \end{aligned}$$

(26)

$$\begin{aligned} r_2 = -\frac{q_k \times N_{ijl} + (N_{ijk} \times q_k)D}{|q_j \times q_k|} - \frac{q_l \times N_{ijk} + (N_{ijl} \times q_l)D}{|q_j \times q_l|} \end{aligned}$$

(27)

$$\begin{aligned} r_3 = \frac{q_j \times N_{ijl} + (N_{ijk} \times q_j)D}{|q_j \times q_k|} \end{aligned}$$

(28)

$$\begin{aligned} r_4 = \frac{q_j \times N_{ijk} + (N_{ijl} \times q_j)D}{|q_j \times q_l|} \end{aligned}$$

(29)

The general final correction for bending constraint is:

$$\begin{aligned} \varDelta q_{i,j,k,l} = -\frac{(\sqrt{1-D^2})(cos^{-1}(D) - \theta _{ijkl})}{|r_1|^2 + |r_2|^2 + |r_3|^2 + |r_4|^2} r_{1,2,3,4} \end{aligned}$$

(30)