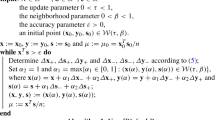Abstract
Interior point methods are one of the popular iterative approaches for solving optimization problems. Search direction plays a vital role in the performance of the interior point methods. This paper uses a modification to the Newton method and proposes a new way to find the search direction. We introduce a two-step interior point algorithm for solving linear optimization problems based on the new search direction. We present theoretical results for the convergence of the algorithm. Finally, we evaluate the algorithm on some test problems from the Netlib collection and show that the proposed algorithm reduces the number of iterations and CPU time by \(30.97\%\) and \(20.46\%\), respectively.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
\(\Vert x\Vert _1=\sum _{i=1}^n|x_i|\).
References
Argyros, I.K., Deep, G., Regmi, S.: Extended Newton-like midpoint method for solving equations in Banach space. Foundations 3(1), 82–98 (2023)
Bai, Y.Q., El Ghami, M., Roos, C.: A comparative study of kernel functions for primal-dual interior-point algorithms in linear optimization. SIAM J. Optim. 15(1), 101–128 (2004)
Cai, X., Wang, G., Zhang, Z.: Complexity analysis and numerical implementation of primal-dual interior-point methods for convex quadratic optimization based on a finite barrier. Numer. Algorithms 62(2), 289–306 (2013)
Fathi-Hafshejani, S., Fakharzadeh Jahromi, A., Peyghami, M.R.: A unified complexity analysis of interior point methods for semidefinite problems based on trigonometric kernel functions. Optimization 67(1), 113–137 (2018)
Fathi-Hafshejani, S., Mansouri, H., Reza Peyghami, M., Chen, S.: Primal-dual interior-point method for linear optimization based on a kernel function with trigonometric growth term. Optimization 67(10), 1605–1630 (2018)
McDougall, T.J., Wotherspoon, S.J.: A simple modification of Newton’s method to achieve convergence of order \(1+\sqrt{2}\). Appl. Math. Lett. 29, 20–25 (2014)
Mehrotra, S.: On the implementation of a primal-dual interior point method. SIAM J. Optim. 2(4), 575–601 (1992)
Monteiro, R.D., Adler, I.: Interior path following primal-dual algorithms. Part I: Linear programming. Math. Program. 44(1–3), 27–41 (1989)
Roos, C.: A full-newton step \(O(n)\) infeasible interior-point algorithm for linear optimization. SIAM J. Optim. 16(4), 1110–1136 (2006)
Roos, C., Terlaky, T., Vial, J.P.: Theory and Algorithms for Linear Optimization: An Interior Point Approach. Wiley, Chichester (1997)
Sonnevend, G.: An “analytical centre’’ for polyhedrons and new classes of global algorithms for linear (smooth, convex) programming. In: Prékopa, A., Szelezsáan, J., Strazicky, B. (eds.) System Modelling and Optimization. LNCIS, vol. 84, pp. 866–875. Springer, Heidelberg (2006). https://doi.org/10.1007/BFb0043914
Terlaky, T., Roos, C., Peng, J.: Self-regularity: A New Paradigm for Primal-Dual Interior-Point Algorithms (Princeton Series in Applied Mathematics). Princeton University Press, Princeton (2002)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
The Appendix section contains two tables. Table 2 specifies information related to each test problem, including the name, the number of non-zero elements, and the number of rows and columns of matrix A. Table 3 provides information on the number of iterations and the CPU time for performing Algorithm 1 and the classical algorithm proposed in [12]. Additionally, the averages of CPU time and the number of iterations from Table 3 are presented in Table 1.
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Hafshejani, S.F., Gaur, D., Benkoczi, R. (2024). An Efficient Interior Point Method for Linear Optimization Using Modified Newton Method. In: Kalyanasundaram, S., Maheshwari, A. (eds) Algorithms and Discrete Applied Mathematics. CALDAM 2024. Lecture Notes in Computer Science, vol 14508. Springer, Cham. https://doi.org/10.1007/978-3-031-52213-0_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-52213-0_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-52212-3
Online ISBN: 978-3-031-52213-0
eBook Packages: Computer ScienceComputer Science (R0)