3D Shape Analysis of Scoliosis

Abstract

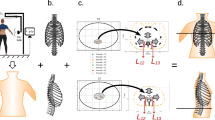
Scoliosis is typically measured in 2D in the coronal plane, although it is a three-dimensional (3D) condition. Our objective in this work is to analyse the 3D geometry of the spine and its relationship to the vertebral canal. To this end, we make three contributions: first, we extract the 3D space curve of the spine automatically from low-resolution whole-body Dixon MRIs and obtain coronal, sagittal and axial projections for various degrees of scoliosis; second, we also extract the vertebral canal as a 3D curve from the MRIs, and examine the relationship between the two 3D curves; and third, we measure the angle of rotation of the spine and examine the correlation between this 3D measurement and the 2D curvature of the coronal projection. For this study, we use 48,384 MRIs from the UK Biobank.

Appendices

Segmentation

There are four separate aligned sequences in the MRI Dixon scans used here. These are in-phase, opposed-phase, fat-only and water-only. The fat-only and water-only sequences are best suited to our task, see Fig. 10. Note, the MRI scans in the UK Biobank have a lower resolution compared to typical clinical spine scans. We segment the spine using axial slices as they have higher resolution, and also support larger receptive fields for training the deep network.

Fig. 10.

Coronal, sagittal and axial projections for fat-only and water-only Dixon MRI sequences.

1.1 Segmentation Network

A U-Net based network architecture is used for the segmentation task [19, 26]. We use a U-Net++ [27] network with a ResNet-34 encoder. The input is 224 $\times$ 160 $\times$ 6, where we stack three adjacent MRI image slices of the spine region for the two MRI sequences (fat-only and water-only). To avoid partial volume effects, and also to benefit from more context, we ingest three adjacent slices, with the middle slice as output. The output has size 224 $\times$ 160 $\times 2$, where 2 refers to the segmentation maps for the spine and vertebral canal.

For training, the loss function is a weighted sum of categorical cross-entropy loss [25] and dice loss [22] computed over a foreground/background/uncertain tri-map to mitigate potentially noisy boundaries in our labels which we define as ± 2px from the foreground boundary. Networks are trained for a maximum of 500 epochs with early stopping when the validation Dice does not increase by $e^{-4}$. We use self-training to leverage the whole training set i.e. n = 38,707. Inspired from the recent work on confirmation bias reduction in self-training [3], we use an independent head for pseudo-label generation to prevent potentially inaccurate pseudo-label backpropagation (Fig. 11).

Fig. 11.

Visualisation of spine and vertebral canal segmentation masks and midpoint curves on the coronal and sagittal plane.

Spline Fitting

1.1 2D Spline Fitting

The 2D projected points (in the coronal or sagittal planes) are approximated by a piecewise cubic spline to smooth out any noise due to sampling. For this fitting, we use the method described in [2].

Using a parametrised curve, we construct polynomial piecewise cubic curves. A single cubic curve has only one inflection point, but scoliosis curves may have one or more. A solution could be to add extra control points and using higher order polynomials. However, higher order polynomials are known to be very sensitive to the locations of the control points. A common alternative in computer vision is to construct cubic curves pieced together with a greater number of inflection points. Each pair of control points form one segment of the curve, where each curve segment is a cubic with its own coefficients.

$$\begin{aligned} f_{i}(x) = a_{i} + b_{i}x + c_{i}x^2 + d_{i}x^3 \end{aligned}$$

(3)

where f is the function representing the curve between control points i and i + 1.

We ensure $C^{0}$, $C^{1}$, $C^{2}$ continuity conditions.

• $C^{0}$: Each segment is required to pass through its control points. That is, $f_{i}$ $(x_{i})$ = $y_{i}$, and $f_{i}$($x_{i+1}$) = $y_{i+1}$

• $C^{1}$: Each curve segment has the same slope at each junction, $f_{i}^{'}$($x_{i+1}$) = $f_{i+1}^{'}$($x_{i+1}$)

• Each curve segment has the same curvature at each junction, $f_{i}^{''}$($x_{i+1}$) = $f_{i+1}^{''}$($x_{i+1}$)

We improve the method in [2] by changing the uniform placement of a fixed number of knots by automatic knot selection using penalised regression splines [20]. The spline curve is composed of $n-1$ piecewise cubic polynomials where n is the total number of knots. The number of knots is selected in the range from 2 to 10.

n is optimised using a penalty to balance goodness-of-fit and smoothness. The selection of knots is such that the model chooses from a bigger selection of functions. As the number of knots increases, the model overfits the data. Too few knots on the other hand gives a more restrictive function.

1.2 3D Spline Fitting

We now extend the 2D spline fitting to three-dimensional space. We have two systems of linear equations for x and y: $M_{x}$ ${\textbf {b}}_{x}$ = x and $M_{y}$ ${\textbf {b}}_{y}$ = y, where b is the vector of curve coefficients, y is the vector of constants, and M is a matrix of continuity conditions i.e. $C^{0}$, $C^{1}$, and $C^{2}$. Each system is solved similarly as in 2D section above, except that we are solving two linear systems instead of one.