Abstract
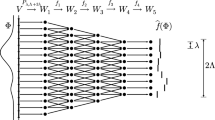
We introduce Equivariant Isomorphic Networks (EquIN) – a method for learning representations that are equivariant with respect to general group actions over data. Differently from existing equivariant representation learners, EquIN is suitable for group actions that are not free, i.e., that stabilize data via nontrivial symmetries. EquIN is theoretically grounded in the orbit-stabilizer theorem from group theory. This guarantees that an ideal learner infers isomorphic representations while trained on equivariance alone and thus fully extracts the geometric structure of data. We provide an empirical investigation on image datasets with rotational symmetries and show that taking stabilizers into account improves the quality of the representations.
L. A. Pérez Rey and G. L. Marchetti—Equal Contribution.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Ahuja, K., Hartford, J., Bengio, Y.: Properties from nechanisms: an equivariance perspective on identifiable representation learning. In: International Conference on Learning Representations (2022)
Bengio, Y., Courville, A., Vincent, P.: Representation learning: a review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35(8), 1798–1828 (2013)
Caselles-Dupré, H., Garcia-Ortiz, M., Filliat, D.: Symmetry-based disentangled representation learning requires interaction with environments. In: Advances in Neural Information Processing Systems (2019)
Chen, R.T., Li, X., Grosse, R.B., Duvenaud, D.K.: Isolating sources of disentanglement in variational autoencoders. In: Advances in Neural Information Processing Systems (2018)
Chen, T., Kornblith, S., Norouzi, M., Hinton, G.: A simple framework for contrastive learning of visual representations. In: International Conference on Machine Learning (2020)
Cohen, T., Welling, M.: Learning the irreducible representations of commutative Lie groups. In: International Conference on Machine Learning (2014)
Dupont, E., Martin, M.B., Colburn, A., Sankar, A., Susskind, J., Shan, Q.: Equivariant neural rendering. In: International Conference on Machine Learning (2020)
Falorsi, L., et al.: Explorations in homeomorphic variational auto-encoding. In: ICML18 Workshop on Theoretical Foundations and Applications of Deep Generative Models (2018)
Guo, X., Zhu, E., Liu, X., Yin, J.: Affine equivariant autoencoder. In: International Joint Conference on Artificial Intelligence (2019)
Ha, D., Schmidhuber, J.: World models. arXiv preprint (2018)
He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: IEEE Conference on Computer Vision and Pattern Recognition (2016)
Higgins, I., et al.: Towards a definition of disentangled representations. arXiv preprint (2018)
Higgins, I., et al.: Beta-VAE: learning basic visual concepts with a constrained variational framework. In: International Conference on Learning Representations (2017)
Higgins, I., Racanière, S., Rezende, D.: Symmetry-based representations for artificial and biological general intelligence. Front. Comput. Neurosci. 16, 836498 (2022)
Hinton, G.E., Krizhevsky, A., Wang, S.D.: Transforming auto-encoders. In: Honkela, T., Duch, W., Girolami, M., Kaski, S. (eds.) ICANN 2011. LNCS, vol. 6791, pp. 44–51. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21735-7_6
Kipf, T., van der Pol, E., Welling, M.: Contrastive learning of structured world models. In: International Conference on Learning Representations (2020)
Liang, K.K.: Efficient conversion from rotating matrix to rotation axis and angle by extending rodrigues’ formula. arXiv preprint (2018)
Locatello, F., et al.: Challenging common assumptions in the unsupervised learning of disentangled representations. In: International Conference on Machine Learning (2019)
Loshchilov, I., Hutter, F.: Decoupled weight decay regularization. In: International Conference on Learning Representations (2019)
Marchand, E., Uchiyama, H., Spindler, F.: Pose estimation for augmented reality: a hands-on survey. IEEE Trans. Vis. Comput. Graph. 22(12), 2633–2651 (2016)
Marchetti, G.L., Tegnér, G., Varava, A., Kragic, D.: Equivariant Representation Learning via Class-Pose Decomposition. arXiv preprint (2022)
Murphy, K., Esteves, C., Jampani, V., Ramalingam, S., Makadia, A.: Implicit representation of probability distributions on the rotation manifold. In: International Conference on Machine Learning (2021)
Painter, M., Hare, J., Prügel-Bennett, A.: Linear disentangled representations and unsupervised action estimation. In: Advances in Neural Information Processing Systems (2020)
Park, J.Y., Biza, O., Zhao, L., van de Meent, J.W., Walters, R.: Learning symmetric embeddings for equivariant world models. In: International Conference on Machine Learning (2022)
van der Pol, E., Kipf, T., Oliehoek, F.A., Welling, M.: Plannable approximations to MDP homomorphisms: equivariance under actions. In: International Conference on Autonomous Agents and Multi-Agent Systems (2020)
Quessard, R., Barrett, T.D., Clements, W.R.: Learning disentangled representations and group structure of dynamical environments. In: Advances in Neural Information Processing Systems (2020)
Rotman, J.J.: An Introduction to the Theory of Groups, vol. 148. Springer, New York (2012). https://doi.org/10.1007/978-1-4612-4176-8
Tonnaer, L., Perez Rey, L.A., Menkovski, V., Holenderski, M., Portegies, J.: Quantifying and learning linear symmetry-based disentanglement. In: International Conference on Machine Learning (2022)
Worrall, D.E., Garbin, S.J., Turmukhambetov, D., Brostow, G.J.: Interpretable transformations with encoder-decoder networks. In: International Conference on Computer Vision (2017)
Wu, Z., et al.: 3D shapenets: a deep representation for volumetric shapes. In: IEEE Conference on Computer Vision and Pattern Recognition (2015)
Acknowledgements
This work was supported by the Swedish Research Council, the Knut and Alice Wallenberg Foundation and the European Research Council (ERC-BIRD-884807). This work has also received funding from the NWO-TTW Programme “Efficient Deep Learning” (EDL) P16-25.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
Ethical Statement
The work presented in this paper consists of a theoretical and practical analysis on learning representations that capture the information about symmetry transformations observed in data. Due to the nature of this work as fundamental research, it is challenging to determine any direct adverse ethical implications that might arise. However, we think that any possible ethical implications of these ideas would be a consequence of the possible applications to augmented reality, object recognition, or reinforcement learning among others. The datasets used in this work consist of procedurally generated images with no personal or sensitive information.
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Pérez Rey, L.A., Marchetti, G.L., Kragic, D., Jarnikov, D., Holenderski, M. (2023). Equivariant Representation Learning in the Presence of Stabilizers. In: Koutra, D., Plant, C., Gomez Rodriguez, M., Baralis, E., Bonchi, F. (eds) Machine Learning and Knowledge Discovery in Databases: Research Track. ECML PKDD 2023. Lecture Notes in Computer Science(), vol 14172. Springer, Cham. https://doi.org/10.1007/978-3-031-43421-1_41
Download citation
DOI: https://doi.org/10.1007/978-3-031-43421-1_41
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43420-4
Online ISBN: 978-3-031-43421-1
eBook Packages: Computer ScienceComputer Science (R0)