Abstract
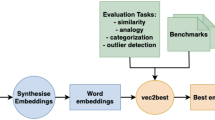
We perform an empirical evaluation of several methods of low-rank approximation in the problem of obtaining PMI-based word embeddings. All word vectors were trained on parts of a large corpus extracted from English Wikipedia (enwik9) which was divided into two equal-sized datasets, from which PMI matrices were obtained. A repeated measures design was used in assigning a method of low-rank approximation (SVD, NMF, QR) and a dimensionality of the vectors (250, 500) to each of the PMI matrix replicates. Our experiments show that word vectors obtained from the truncated SVD achieve the best performance on two downstream tasks, similarity and analogy, compare to the other two low-rank approximation methods.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Assume that words have already been converted into integer indices.
- 2.
\(\textbf{A}_{a:b,c:d}\) is a submatrix located at the intersection of rows \(a, a+1, \ldots , b\) and columns \(c, c + 1, \ldots , d\) of a matrix \(\textbf{A}\).
- 3.
- 4.
The isotropy is motivated by the work of Arora et al. (2016); \(\mathbf {4.5}\) is a vector with all elements equal to 4.5.
References
Arora, S., Li, Y., Liang, Y., Ma, T., Risteski, A.: A latent variable model approach to PMI-based word embeddings. Trans. Assoc. Comput. Linguist. 4, 385–399 (2016)
Davis, T.A., Hu, Y.: The university of Florida sparse matrix collection. ACM Trans. Math. Softw. (TOMS) 38(1), 1 (2011)
Eckart, C., Young, G.: The approximation of one matrix by another of lower rank. Psychometrika 1(3), 211–218 (1936)
Finkelstein, L., et al.: Placing search in context: the concept revisited. ACM Trans. Inf. Syst. 20(1), 116–131 (2002)
Jones, E., Oliphant, T., Peterson, P.: \(\{\)SciPy\(\}\): open source scientific tools for \(\{\)Python\(\}\) (2014)
Kishore Kumar, N., Schneider, J.: Literature survey on low rank approximation of matrices. Linear Multilinear Algebra 65(11), 2212–2244 (2017)
Levy, O., Goldberg, Y.: Neural word embedding as implicit matrix factorization. In: Advances in Neural Information Processing Systems, pp. 2177–2185 (2014)
Levy, O., Goldberg, Y., Dagan, I.: Improving distributional similarity with lessons learned from word embeddings. TACL 3, 211–225 (2015)
Mikolov, T., Sutskever, I., Chen, K., Corrado, G.S., Dean, J.: Distributed representations of words and phrases and their compositionality. In: Advances in Neural Information Processing Systems, pp. 3111–3119 (2013)
Pedregosa, F., et al.: Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12(Oct), 2825–2830 (2011)
Acknowledgement
The work of Zhenisbek Assylbekov has been funded by the Committee of Science of the Ministry of Education and Science of the Republic of Kazakhstan, contract # 346/018-2018/33-28, IRN AP05133700.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 Springer Nature Switzerland AG
About this paper
Cite this paper
Sorokina, A., Karipbayeva, A., Assylbekov, Z. (2023). Low-Rank Approximation of Matrices for PMI-Based Word Embeddings. In: Gelbukh, A. (eds) Computational Linguistics and Intelligent Text Processing. CICLing 2019. Lecture Notes in Computer Science, vol 13451. Springer, Cham. https://doi.org/10.1007/978-3-031-24337-0_7
Download citation
DOI: https://doi.org/10.1007/978-3-031-24337-0_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-24336-3
Online ISBN: 978-3-031-24337-0
eBook Packages: Computer ScienceComputer Science (R0)