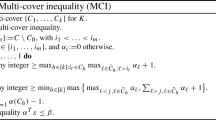Abstract
The complementarity knapsack problem (CKP) is a knapsack problem with real-valued variables and complementarity conditions between pairs of its variables. We extend the polyhedral studies of De Farias et al. for CKP, by proposing three new families of cutting-planes that are all obtained from a combinatorial concept known as a pack. Sufficient conditions for these inequalities to be facet-defining, based on the concept of a maximal switching pack, are also provided. Moreover, we answer positively a conjecture by De Farias et al. about the separation complexity of the inequalities introduced in their work.
A. Del Pia is partially funded by ONR grant N00014-19–1-2322. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the Office of Naval Research.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
These are not the typical “cover inequalities” in 0–1 programming.
References
Atamtürk, A.: Cover and pack inequalities for (mixed) integer programming. Ann. Oper. Res. 139(1), 21–38 (2005)
Balas, E.: Facets of the knapsack polytope. Math. Program. 8(1), 146–164 (1975)
Balas, E., Zemel, E.: Facets of the knapsack polytope from minimal covers. SIAM J. Appl. Math. 34(1), 119–148 (1978)
Beale, E.M.L., Tomlin, J.A.: Special facilities in a general mathematical programming system for non-convex problems using ordered sets of variables. OR 69(447–454), 99 (1970)
Beaumont, N.: An algorithm for disjunctive programs. Eur. J. Oper. Res. 48(3), 362–371 (1990)
Crowder, H., Johnson, E.L., Padberg, M.: Solving large-scale zero-one linear programming problems. Oper. Res. 31(5), 803–834 (1983)
De Farias, I., Johnson, E.L., Nemhauser, G.L.: Branch-and-cut for combinatorial optimization problems without auxiliary binary variables. Knowl. Eng. Rev. 16(1), 25–39 (2001)
De Farias Jr, I.R., Johnson, E.L., Nemhauser, G.L.: Facets of the complementarity knapsack polytope. Math. Oper. Res. 27(1), 210–226 (2002)
Del Pia, A., Linderoth, J., Zhu, H.: Multi-cover inequalities for totally-ordered multiple knapsack sets. In: International Conference on Integer Programming and Combinatorial Optimization, pp. 193–207. Springer, Heidelberg (2021). https://doi.org/10.1007/s10107-022-01817-4
Del Pia, A., Linderoth, J., Zhu, H.: Multi-cover inequalities for totally-ordered multiple knapsack sets: theory and computation. arXiv preprint arXiv:2106.00301 (2021)
Del Pia, A., Linderoth, J., Zhu, H.: On the complexity of separation from the Knapsack Polytope. In: International Conference on Integer Programming and Combinatorial Optimization, pp. 168–180. Springer, Cham
de Farias, I.R., Kozyreff, E., Zhao, M.: Branch-and-cut for complementarity-constrained optimization. Math. Program. Comput. 6(4), 365–403 (2014). https://doi.org/10.1007/s12532-014-0070-2
de Farias, I.R., Zhao, M.: A polyhedral study of the semi-continuous knapsack problem. Math. Program. 142(1–2), 169–203 (2013)
Fischer, T., Pfetsch, M.E.: Branch-and-cut for linear programs with overlapping SOS1 constraints. Math. Program. Comput. 10(1), 33–68 (2018)
Gu, Z., Nemhauser, G.L., Savelsbergh, M.W.P.: Lifted cover inequalities for \(0\text{- }1\) integer programs: complexity. INFORMS J. Comput. 11(1), 117–123 (1999)
Gu, Z., Nemhauser, G.L., Savelsbergh, M.W.: Lifted cover inequalities for 0–1 integer programs: computation. INFORMS J. Comput. 10(4), 427–437 (1998)
Gu, Z., Nemhauser, G.L., Savelsbergh, M.W.: Sequence independent lifting in mixed integer programming. J. Comb. Optim. 4(1), 109–129 (2000)
Hojny, C., Gally, T., Habeck, O., Lüthen, H., Matter, F., Pfetsch, M.E., Schmitt, A.: Knapsack polytopes: a survey. Ann. Oper. Res. 292, 1–49 (2019)
Karp, R.M.: Reducibility among combinatorial problems. In: Complexity of Computer Computations, pp. 85–103 (1972)
Keha, A.B., de Farias Jr, I.R., Nemhauser, G.L.: A branch-and-cut algorithm without binary variables for nonconvex piecewise linear optimization. Oper. Res. 54(5), 847–858 (2006)
Klabjan, D., Nemhauser, G.L., Tovey, C.: The complexity of cover inequality separation. Oper. Res. Lett. 23(1–2), 35–40 (1998)
Padberg, M.W.: (1, k)-configurations and facets for packing problems. Math. Program. 18(1), 94–99 (1980)
Weismantel, R.: On the 0/1 knapsack polytope. Math. Program. 77(3), 49–68 (1997)
Wolsey, L.A.: Faces for a linear inequality in 0–1 variables. Math. Program. 8(1), 165–178 (1975)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Del Pia, A., Linderoth, J., Zhu, H. (2022). New Classes of Facets for Complementarity Knapsack Problems. In: Ljubić, I., Barahona, F., Dey, S.S., Mahjoub, A.R. (eds) Combinatorial Optimization. ISCO 2022. Lecture Notes in Computer Science, vol 13526. Springer, Cham. https://doi.org/10.1007/978-3-031-18530-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-031-18530-4_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-18529-8
Online ISBN: 978-3-031-18530-4
eBook Packages: Computer ScienceComputer Science (R0)