Abstract
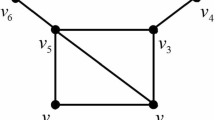
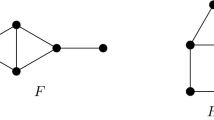
Finding an optimal fast search strategy for graphs is challenging, sometimes even when graphs have very small treewidth, like cacti, cartesian product of a tree and an edge, etc. However, it may be easier to find an optimal fast search strategy for some critical subgraphs of the given graph. Although fast searching is not subgraph-closed, this observation still motivates us to establish relationships between optimal fast search strategies for a graph and its subgraphs. In this paper, we introduce the notion of k-combinable graphs and propose a new method for computing their fast search number. Assisted by the new method, we investigate the fast search number of cacti graphs and the cartesian product of a tree and an edge. Algorithms for producing fast search strategies for the above graphs, along with rigorous proofs, are given in this paper.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bienstock, D.: Graph searching, path-width, tree-width and related problems (a survey). DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 5, 33–49 (1991)
Bonato, A., Yang, B.: Graph searching and related problems. In: Pardalos, P.M., Du, D.-Z., Graham, R.L. (eds.) Handbook of Combinatorial Optimization, pp. 1511–1558. Springer, New York (2013). https://doi.org/10.1007/978-1-4419-7997-1_76
Breisch, R.: An intuitive approach to speleotopology. Southwestern Cavers 6(5), 72–78 (1967)
Dereniowski, D., Diner, Ö., Dyer, D.: Three-fast-searchable graphs. Discret. Appl. Math. 161(13), 1950–1958 (2013)
Dyer, D., Yang, B., Yaşar, Ö.: On the fast searching problem. In: Fleischer, R., Xu, J. (eds.) AAIM 2008. LNCS, vol. 5034, pp. 143–154. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-68880-8_15
Fomin, F.V., Thilikos, D.M.: An annotated bibliography on guaranteed graph searching. Theoret. Comput. Sci. 399(3), 236–245 (2008)
Makedon, F.S., Papadimitriou, C.H., Sudborough, I.H.: Topological bandwidth. SIAM J. Algebraic Discrete Methods 6(3), 418–444 (1985)
Megiddo, N., Hakimi, S.L., Garey, M.R., Johnson, D.S., Papadimitrioum, C.H.: The complexity of searching a graph. J. ACM 35(1), 18–44 (1988)
Parsons, T.: Pursuit-evasion in a graph. In: Proceedings of the International Conference on the Theory and Applications of Graphs, pp. 426–441. Springer-Verlag (1976). https://doi.org/10.1007/BFb0070400
Stanley, D., Yang, B.: Fast searching games on graphs. J. Comb. Optim. 22(4), 763–777 (2011)
Xue, Y., Yang, B.: The fast search number of a cartesian product of graphs. Discret. Appl. Math. 224, 106–119 (2017)
Xue, Y., Yang, B., Zhong, F., Zilles, S.: The fast search number of a complete \(k\)-partite graph. Algorithmica 80(12), 3959–3981 (2018)
Yang, B.: Fast edge searching and fast searching on graphs. Theoret. Comput. Sci. 412(12), 1208–1219 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Xue, Y., Yang, B., Zilles, S. (2022). Fast Searching on k-Combinable Graphs. In: Ni, Q., Wu, W. (eds) Algorithmic Aspects in Information and Management. AAIM 2022. Lecture Notes in Computer Science, vol 13513. Springer, Cham. https://doi.org/10.1007/978-3-031-16081-3_34
Download citation
DOI: https://doi.org/10.1007/978-3-031-16081-3_34
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-16080-6
Online ISBN: 978-3-031-16081-3
eBook Packages: Computer ScienceComputer Science (R0)