Strong Cliques in Diamond-Free Graphs | SpringerLink
Skip to main content
Springer Nature Link
Log in

Strong Cliques in Diamond-Free Graphs

  • Conference paper
  • First Online:
Graph-Theoretic Concepts in Computer Science (WG 2020)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 12301))

Included in the following conference series:

  • 519 Accesses

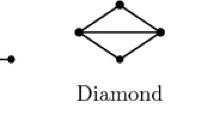
Abstract

A strong clique in a graph is a clique intersecting all inclusion-maximal stable sets. Strong cliques play an important role in the study of perfect graphs. We study strong cliques in the class of diamond-free graphs, from both structural and algorithmic points of view. We show that the following five NP-hard or co-NP-hard problems remain intractable when restricted to the class of diamond-free graphs: Is a given clique strong? Does the graph have a strong clique? Is every vertex contained in a strong clique? Given a partition of the vertex set into cliques, is every clique in the partition strong? Can the vertex set be partitioned into strong cliques?

On the positive side, we show that the following two problems whose computational complexity is open in general can be solved in linear time in the class of diamond-free graphs: Is every maximal clique strong? Is every edge contained in a strong clique? These results are derived from a characterization of diamond-free graphs in which every maximal clique is strong, which also implies an improved Erdős-Hajnal property for such graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 5719
Price includes VAT (Japan)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 7149
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    In  [25], the authors state that the two problems are NP-hard, but their proof actually shows co-NP-hardness.

References

  1. Alcón, L., Gutierrez, M., Kovács, I., Milanič, M., Rizzi, R.: Strong cliques and equistability of EPT graphs. Discret. Appl. Math. 203, 13–25 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alcón, L., Gutierrez, M., Milanič, M.: A characterization of claw-free CIS graphs and new results on the order of CIS graphs. Electron. Notes Theoret. Comput. Sci. 346, 15–27 (2019)

    Article  Google Scholar 

  3. Alekseev, V.E.: On the number of maximal independent sets in graphs from hereditary classes. In: Combinatorial-Algebraic Methods in Discrete Optimization, pp. 5–8. University of Nizhny Novgorod (1991). (in Russian)

    Google Scholar 

  4. Andrade, D.V., Boros, E., Gurvich, V.: Not complementary connected and not CIS \(d\)-graphs form weakly monotone families. Discret. Math. 310(5), 1089–1096 (2010)

    MathSciNet  MATH  Google Scholar 

  5. Andrade, D.V., Boros, E., Gurvich, V.: On graphs whose maximal cliques and stable sets intersect. In: Goldengorin, B. (ed.) Optimization Problems in Graph Theory. SOIA, vol. 139, pp. 3–63. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94830-0_2

    Chapter  Google Scholar 

  6. Balas, E., Yu, C.S.: On graphs with polynomially solvable maximum-weight clique problem. Networks 19(2), 247–253 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  7. Berge, C., Chvátal, V. (eds.): Topics on Perfect Graphs. North-Holland Mathematics Studies, vol. 88. North-Holland Publishing Co., Amsterdam (1984)

    MATH  Google Scholar 

  8. Berge, C., Duchet, P.: Strongly perfect graphs. In: Topics on Perfect Graphs. North-Holland Mathematics Studies, vol. 88, pp. 57–61. North-Holland, Amsterdam (1984)

    Google Scholar 

  9. Boros, E., Gurvich, V., Milanič, M.: On CIS circulants. Discrete Math. 318, 78–95 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Boros, E., Gurvich, V., Milanič, M.: On equistable, split, CIS, and related classes of graphs. Discret. Appl. Math. 216(part 1), 47–66 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. Brandstädt, A., Giakoumakis, V., Maffray, F.: Clique separator decomposition of hole-free and diamond-free graphs and algorithmic consequences. Discret. Appl. Math. 160(4–5), 471–478 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cheston, G.A., Hare, E.O., Hedetniemi, S.T., Laskar, R.C.: Simplicial graphs. In: 1988 19th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Baton Rouge, LA, vol. 67, pp. 105–113 (1988)

    Google Scholar 

  13. Cheston, G.A., Jap, T.S.: A survey of the algorithmic properties of simplicial, upper bound and middle graphs. J. Graph Algorithms Appl. 10(2), 159–190 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  14. Chudnovsky, M.: The Erdös-Hajnal conjecture-a survey. J. Graph Theor. 75(2), 178–190 (2014)

    Article  MATH  Google Scholar 

  15. Chudnovsky, M., Goedgebeur, J., Schaudt, O., Zhong, M.: Obstructions for three-coloring graphs without induced paths on six vertices. J. Combin. Theory Ser. B 140, 45–83 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. Chvátal, V., Slater, P.J.: A note on well-covered graphs. In: Quo Vadis, Graph Theory? Annals of Discrete Mathematics, vol. 55, pp. 179–181. North-Holland, Amsterdam (1993)

    Google Scholar 

  17. Dabrowski, K.K., Dross, F., Paulusma, D.: Colouring diamond-free graphs. J. Comput. Syst. Sci. 89, 410–431 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  18. Deng, X., Li, G., Zang, W.: Proof of Chvátal’s conjecture on maximal stable sets and maximal cliques in graphs. J. Combin. Theor. Ser. B 91(2), 301–325 (2004)

    Article  MATH  Google Scholar 

  19. Dobson, E., Hujdurović, A., Milanič, M., Verret, G.: Vertex-transitive CIS graphs. Eur. J. Combin. 44(part A), 87–98 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. Erdős, P., Hajnal, A.: Ramsey-type theorems. Discret. Appl. Math. 25(1–2), 37–52 (1989). Combinatorics and complexity (Chicago, IL, 1987)

    Article  MathSciNet  MATH  Google Scholar 

  21. Gurvich, V.: On exact blockers and anti-blockers, \(\Delta \)-conjecture, and related problems. Discret. Appl. Math. 159(5), 311–321 (2011)

    MathSciNet  MATH  Google Scholar 

  22. Gyárfás, A.: Reflections on a problem of Erdős and Hajnal. In: Graham, R.L., Nesetril, J. (eds.) The Mathematics of Paul Erdős, II. Algorithms and Combinatorics, vol. 14, pp. 93–98. Springer, New York (1997). https://doi.org/10.1007/978-1-4614-7254-4_11

    Chapter  MATH  Google Scholar 

  23. Hoàng, C.T.: Efficient algorithms for minimum weighted colouring of some classes of perfect graphs. Discret. Appl. Math. 55(2), 133–143 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  24. Hujdurović, A., Milanič, M., Ries, B.: Graphs vertex-partitionable into strong cliques. Discret. Math. 341(5), 1392–1405 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hujdurović, A., Milanič, M., Ries, B.: Detecting strong cliques. Discret. Math. 342(9), 2738–2750 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  26. Kamiński, M., Lozin, V.: Coloring edges and vertices of graphs without short or long cycles. Contrib. Discret. Math. 2(1), 61–66 (2007)

    MathSciNet  MATH  Google Scholar 

  27. Karthick, T., Mishra, S.: On the chromatic number of (\(P_6\), diamond)-free graphs. Graphs Combin. 34(4), 677–692 (2018)

    MathSciNet  MATH  Google Scholar 

  28. Kloks, T., Lee, C.-M., Liu, J., Müller, H.: On the recognition of general partition graphs. In: Bodlaender, H.L. (ed.) WG 2003. LNCS, vol. 2880, pp. 273–283. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-39890-5_24

    Chapter  Google Scholar 

  29. Kloks, T., Müller, H., Vušković, K.: Even-hole-free graphs that do not contain diamonds: a structure theorem and its consequences. J. Combin. Theor. Ser. B 99(5), 733–800 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. McAvaney, K., Robertson, J., DeTemple, D.: A characterization and hereditary properties for partition graphs. Discret. Math. 113(1–3), 131–142 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  31. Milanič, M., Trotignon, N.: Equistarable graphs and counterexamples to three conjectures on equistable graphs. J. Graph Theor. 84(4), 536–551 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  32. Prisner, E.: Graphs with few cliques. In: Alavi, Y., Schwenk, A. (eds.) Graph Theory, Combinatorics, and Algorithms: Proceedings of 7th Quadrennial International Conference on the Theory and Applications of Graphs, Western Michigan University, pp. 945–956. Wiley, New York (1995)

    Google Scholar 

  33. Sankaranarayana, R.S., Stewart, L.K.: Complexity results for well-covered graphs. Networks 22(3), 247–262 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  34. Skowrońska, M., Sysło, M.M.: An algorithm to recognize a middle graph. Discret. Appl. Math. 7(2), 201–208 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  35. Tsukiyama, S., Ide, M., Ariyoshi, H., Shirakawa, I.: A new algorithm for generating all the maximal independent sets. SIAM J. Comput. 6(3), 505–517 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  36. Tucker, A.: Coloring perfect \((K_4-e)\)-free graphs. J. Combin. Theor. Ser. B 42, 313–318 (1987)

    MATH  Google Scholar 

  37. Zang, W.: Generalizations of Grillet’s theorem on maximal stable sets and maximal cliques in graphs. Discret. Math. 143(1–3), 259–268 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  38. Zverovich, I., Zverovich, I.: Bipartite bihypergraphs: a survey and new results. Discret. Math. 306(8–9), 801–811 (2006)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to Ademir Hujdurović for helpful discussions and the anonymous reviewers for constructive remarks. The second named author has been supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 734922, by Mexico’s CONACYT scholarship 254379/438356, by Erasmus+ for practices (SMT) Action KA103 - Project 2017/2019, by MICINN from the Spanish Government under project PGC2018-095471-B-I00, and by AGAUR from the Catalan Government under project 2017SGR1087. The first and third named authors are supported in part by the Slovenian Research Agency (I0-0035, research programs P1-0285 and P1-0404, and research projects J1-9110, N1-0102, N1-0160). Part of this work was done while the third named author was visiting LAMSADE, University Paris-Dauphine; their support and hospitality is gratefully acknowledged.

Author information

Authors and Affiliations

  1. FAMNIT, University of Primorska, Koper, Slovenia

    Nina Chiarelli, Martin Milanič & Peter Muršič

  2. IAM, University of Primorska, Koper, Slovenia

    Nina Chiarelli & Martin Milanič

  3. Departament d’Enginyeria Civil i Ambiental, Universitat Politècnica de Catalunya, Barcelona, Spain

    Berenice Martínez-Barona

  4. LAMSADE, University Paris-Dauphine, Paris Cedex 16, France

    Jérôme Monnot

Authors
  1. Nina Chiarelli
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Berenice Martínez-Barona
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Martin Milanič
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jérôme Monnot
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Peter Muršič
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin Milanič .

Editor information

Editors and Affiliations

  1. University of Leeds, Leeds, UK

    Isolde Adler

  2. University of Leeds, Leeds, UK

    Haiko Müller

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Chiarelli, N., Martínez-Barona, B., Milanič, M., Monnot, J., Muršič, P. (2020). Strong Cliques in Diamond-Free Graphs. In: Adler, I., Müller, H. (eds) Graph-Theoretic Concepts in Computer Science. WG 2020. Lecture Notes in Computer Science(), vol 12301. Springer, Cham. https://doi.org/10.1007/978-3-030-60440-0_21

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-60440-0_21

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-60439-4

  • Online ISBN: 978-3-030-60440-0

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation