Abstract
Chemical reaction networks (CRNs) and DNA strand displacement systems have shown potential for implementing logically and physically reversible computation. It has been shown that CRNs on a surface allow highly scalable and parallelizable computation. In this paper, we demonstrate that simple rearrangement reactions on a surface, which we refer to as swaps, are capable of physically reversible Boolean computation. We present designs for elementary logic gates, a method for constructing arbitrary feedforward digital circuits, and a proof of their correctness.
T. Brailovskaya, G. Gowri and S. Yu—Equal contribution.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Landauer, R.: Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 5, 183–191 (1961)
Bennett, C.H.: Logical reversibility of computation. IBM J. Res. Dev. 17, 525–532 (1973)
Fredkin, E., Toffoli, T.: Conservative logic. Int. J. Theor. Phys. 21, 219–253 (1982)
Margolus, N.: Physics-like models of computation. Phys. D Nonlinear Phenom. 10, 81–95 (1984)
D’Souza, R.M., Homsy, G.E., Margolus, N.H.: Simulating digital logic with the reversible aggregation model of crystal growth. In: Griffeath, D., Moore, C. (eds.) New Constructions in Cellular Automata, pp. 211–230. Oxford University Press, Oxford (2003)
Ouldridge, T.E.: The importance of thermodynamics for molecular systems, and the importance of molecular systems for thermodynamics. Nat. Comput. 17, 3–29 (2018)
Wolpert, D.: The stochastic thermodynamics of computation. J. Phys. Math. Theor. 52, 193001 (2019)
Perumalla, K.S.: Introduction to Reversible Computing. Chapman and Hall/CRC, Boca Raton (2013)
Bennett, C.H.: The thermodynamics of computation-a review. Int. J. Theor. Phys. 21, 905–940 (1982)
Soloveichik, D., Seelig, G., Winfree, E.: DNA as a universal substrate for chemical kinetics. Proc. Natl. Acad. Sci. 107, 5393–5398 (2010)
Chen, Y.-J., et al.: Programmable chemical controllers made from DNA. Nat. Nanotechnol. 8, 755–762 (2013)
Srinivas, N., Parkin, J., Seelig, G., Winfree, E., Soloveichik, D.: Enzyme-free nucleic acid dynamical systems. Science 358, eaal2052 (2017)
Thachuk, C., Condon, A.: Space and energy efficient computation with DNA strand displacement systems. In: Stefanovic, D., Turberfield, A. (eds.) DNA 2012. LNCS, vol. 7433, pp. 135–149. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32208-2_11
Codon, A., Hu, A.J., Manuch, J., Thachuk, C.: Less haste, less waste: on recycling and its limits in strand displacement systems. Interface Focus 2, 512–521 (2012)
Condon, A., Thachuk, C.: Towards space- and energy-efficient computations. In: Kempes, C., Grochow, J., Stadler, P., Wolpert, D. (eds.) The Energetics of Computing in Life and Machines, Chap. 9, pp. 209–232. The Sante Fe Institute Press, Sante Fe (2019)
Qian, L., Soloveichik, D., Winfree, E.: Efficient turing-universal computation with DNA polymers. In: Sakakibara, Y., Mi, Y. (eds.) DNA 2010. LNCS, vol. 6518, pp. 123–140. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18305-8_12
Qian, L., Winfree, E.: Parallel and scalable computation and spatial dynamics with DNA-based chemical reaction networks on a surface. In: Murata, S., Kobayashi, S. (eds.) DNA 2014. LNCS, vol. 8727, pp. 114–131. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11295-4_8
Goldschlager, L.M.: The monotone and planar circuit value problems are log space complete for P. ACM SIGACT News 9, 25–29 (1977)
Masson, G.M., Gingher, G.C., Nakamura, S.: A sampler of circuit switching networks. Computer 12, 32–48 (1979)
Savage, J.E.: Models of Computation. Addison-Wesley, Reading (1998). Section 12.6
Qian, L., Winfree, E.: Scaling up digital circuit computation with DNA strand displacement cascades. Science 332, 1196–1201 (2011)
Milner, R.: Communication and Concurrency. Prentice Hall, Upper Saddle River (1989)
Johnson, R.F., Dong, Q., Winfree, E.: Verifying chemical reaction network implementations: a bisimulation approach. Theor. Comput. Sci. 765, 3–46 (2019)
Acknowledgements
Support from National Science Foundation grant CCF-1317694 is gratefully acknowledged. We also thank Lulu Qian and Chris Thachuk for helpful discussion and comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
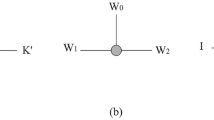
Paint functions for the NOT gate. All species in the stochastic CRN that corresponds to the NOT gate as well as their associated paint functions are shown. In each table, the left hand column is the list of species. Each row is a paint function for a particular species. Each column represents how a particular lattice is painted. (a) Initial configuration of the NOT gate with each lattice point labeled with a row number and a column letter. (b) Paint function for B. (c) Paint function for \(A^{(0)}\) including \(A_S\). (d) Paint function for \(A^{(1)}\) excluding \(A_S\). (e) Stochastic CRN equivalent to the NOT gate.
Paint functions and the stochastic CRN for the AND gate. (a) Initial AND gate surface layout with each lattice labeled with a row number and a column letter. (b) Paint function for \(A^{(1)}\). (c) Paint function for D. (d) Paint function for B. (e) Paint function for C. (f) Paint function for \(A^{(0)}\). (g) Stochastic CRN equivalent to AND gate.
Paint functions for the fanout gate. (a) Initial configuration of the fanout gate with each lattice labeled with a row number and a column letter. (b) Paint function for A. (c) Paint function for B. (d) Paint function for \(C^{(1)}\) including \(C_S\). (e) Paint function for \(C^{(0)}\) excluding \(C_S\). (f) Stochastic CRN equivalent to fanout.
Paint function for partial wirecross. Truncated portions are equivalent to trajectories found in AND/OR/NOT gates. (a) Initial configuration of the central portion of wirecross with each lattice labeled with a row number and a column letter. (b) Paint function for A. (c) Paint function for B. (d) Paint function for C. (e) Paint function for D. (f) Stochastic CRN equivalent to central portion of wirecross.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Brailovskaya, T., Gowri, G., Yu, S., Winfree, E. (2019). Reversible Computation Using Swap Reactions on a Surface. In: Thachuk, C., Liu, Y. (eds) DNA Computing and Molecular Programming. DNA 2019. Lecture Notes in Computer Science(), vol 11648. Springer, Cham. https://doi.org/10.1007/978-3-030-26807-7_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-26807-7_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26806-0
Online ISBN: 978-3-030-26807-7
eBook Packages: Computer ScienceComputer Science (R0)