Abstract
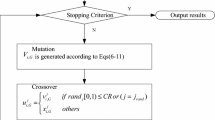
In this paper, second order differential evolution (SODE) algorithm is considered to solve the constrained optimization problems. After offspring are generated by the second order differential evolution, the ε constrained method is chosen for selection in this paper. In order to show that second order differential vector is better than differential vector in solving constrained optimization problems, differential evolution (DE) with the ε constrained method is used for performance comparison. The experiments on 12 test functions from IEEE CEC 2006 demonstrate that second order differential evolution shows better or at least competitive performance against DE when dealing with constrained optimization problems.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Storn, R., Price, K.: Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 11(4), 341–359 (1997)
Harno, H.G., Petersen, I.R.: Synthesis of linear coherent quantum control systems using a differential evolution algorithm. IEEE Trans. Autom. Control 60(3), 799–805 (2015)
Chiu, W.-Y.: Pareto optimal controller designs in differential games. In: 2014 CACS International Automatic Control Conference (CACS), pp. 179–184. IEEE (2014)
Wei, W., Wang, J., Tao, M.: Constrained differential evolution with multiobjective sorting mutation operators for constrained optimization. Appl. Soft Comput. 33, 207–222 (2015)
Zhao, X., Xu, G., Liu, D., Zuo, X.: Second order differential evolution algorithm. CAAI Trans. Intell. Technol. 2, 96–116 (2017)
Takahama, T., Sakai, S.: Constrained optimization by the ε constrained differential evolution with an archive and gradient-based mutation. In: IEEE Congress on Evolutionary Computation, pp. 1–9. IEEE (2010)
Takahama, T., Sakai, S.: Efficient constrained optimization by the constrained rank based differential evolution. In: 2012 IEEE Congress on Evolutionary Computation, pp. 1–8. IEEE (2012)
Wang, B.C., Li, H.X., Li, J.P., Wang, Y.: Composite differential evolution for constrained evolutionary optimization. IEEE Trans. Syst. Man Cybernet. Syst. 99, 1–14 (2018)
Liang, J., et al.: Problem definitions and evaluation criteria for the CEC 2006 special session on constrained real-parameter optimization. J. Appl. Mech. 41(8), 8–31 (2006)
Li, Z.Y., Huang, T., Chen, S.M., Li, R.F.: Overview of constrained optimization evolutionary algorithms. J. Softw. 28(6), 1529–1546 (2017)
Wang, Y., Cai, Z.X., Zhou, Y.R., Xiao, C.X.: Constrained optimization evolutionary algorithms. J. Softw. 20(1), 11–29 (2009)
Acknowledgments
This research is supported by National Natural Science Foundation of China (71772060, 61873040, 61375066). We will express our awfully thanks to the Swarm Intelligence Research Team of BeiYou University.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Zhao, X., Liu, J., Hao, J., Chen, J., Zuo, X. (2019). Second Order Differential Evolution for Constrained Optimization. In: Tan, Y., Shi, Y., Niu, B. (eds) Advances in Swarm Intelligence. ICSI 2019. Lecture Notes in Computer Science(), vol 11655. Springer, Cham. https://doi.org/10.1007/978-3-030-26369-0_36
Download citation
DOI: https://doi.org/10.1007/978-3-030-26369-0_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26368-3
Online ISBN: 978-3-030-26369-0
eBook Packages: Computer ScienceComputer Science (R0)