Abstract
An atmospheric and marine computational forecasting system for Guanabara Bay (GB) was developed to support the Brazilian Sailing Teams in the 2016 Olympic and Paralympic Games. This system, operational since August 2014, is composed of the Weather Research and Forecasting (WRF) and the Regional Ocean Modeling System (ROMS) models, which are both executed daily, yielding 72-h prognostics. The WRF model uses the Global Forecast System (GFS) as the initial and boundary conditions, configured with a three nested-grid scheme. The ocean model is also configured using three nested grids, obtaining atmospheric fields from the implemented WRF and ocean forecasts from CMEMS and TPXO7.2 as tidal forcing. To evaluate the model performances, the atmospheric results were compared with data from two local airports, and the ocean model results were compared with data collected from an acoustic current profiler and tidal prediction series obtained from harmonic constants at four stations located in GB. According to the results, reasonable model performances were obtained in representing marine currents, sea surface heights and surface winds. The system could represent the most important local atmospheric and oceanic conditions, being suitable for nautical applications.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The application of environmental information to sports has become a common practice in the last two decades, especially regarding the Olympic Games (e.g., Powell and Rinard 1998; Horel et al. 2002; Golding et al. 2014). The sport of sailing is extremely sensitive to weather conditions, as wind is a limiting factor for the occurrence of yachting events, and a lack of wind can make it impossible to practice the sport. In this sense, forecasts are required to provide information to manage competition schedules and establish strategies for better performance of athletes during nautical competitions. For sailing, oceanic and atmospheric models have been employed to provide wind and sea surface current forecasts (Powell and Rinard 1998; Katzfey and McGregor 2005; Vermeersch and Alcoforado 2013). These predictions have been used to support the Olympic and Paralympic Games, as weather has become an important issue in terms of planning, training and safety (Powell and Rinard 1998; Rothfusz et al. 1998; Spark and Connor 2004; Golding et al. 2014).
The Brazilian Olympic Games were held in the period between August 5 to 21, 2016, and the Paralympic Games were held from September 7 to 18, 2016 in Rio de Janeiro. Nautical sports occurred mainly in Guanabara Bay (GB), located in the metropolitan region. A regional forecast system with ocean and atmospheric models for the GB was developed to support the Brazilian Olympic Sailing Team during the 2016 Olympic Games and during prior training and official test events. This system consisted of two numerical models that yield wind, sea surface height and current forecasts, which then became available to Brazilian coaches and athletes.
The goal of the present paper is to evaluate the modelling system considering atmospheric and oceanic data collected in situ and to provide an overview of the computational modelling forecast system applied to GB.
2 Study Area
GB is one of the most important coastal marine environments in Brazil due to its economic, social and political characteristics. This bay is located near the second largest Brazilian metropolitan region, surrounded by Rio de Janeiro, Niterói, Sao Gonçalo, Magé and Duque de Caxias municipalities. There are two oil refineries, the second largest Brazilian port and two international airports in the metropolitan area around GB. The bay constitutes an important marine traffic area for many commercial and fishery ships and vessels. The importance of the bay was highlighted during the 2016 Olympic and Paralympic Games by its use as the main area for Olympic sailing competitions.
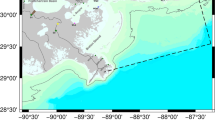
GB is located between 22.68° S and 22.97° S latitude and 43.03° W and 43.30° W longitude (Fig. 1), covering an area of 384 km2. Its longitudinal length is approximately 30 km, with a zonal length of approximately 28 km. There are several islands located inside the bay, which cover an area of almost 60 km2. The average depth of the entire bay is approximately 4 m, but in the main navigation channel, depths of approximately 50 m are found (Kjerfve et al. 1997). The shallower regions are in GB’s northern area, which is directly influenced by river and sediment discharges.
Bathymetry of the oceanic grid domain G2 (color shading) and position of atmospheric (square dots) and oceanic stations used for the model performance evaluation. The circles represent the tidal stations, and the triangle marks the ADCP location. The G2 location is shown in Fig. 2. (Color figure online)
The river basin that flows into GB contains 45 rivers and streams, corresponding to an annual average flow of 100 m3/s. Nevertheless, the continental water volume is small compared to the water volume of the bay and to the marine water inputs. The most important rivers that flow into GB are located in the northern part of the bay (Fig. 1). December and July are the months with the highest and lowest average discharge, respectively, which demonstrates the semiannual variability of the river discharge in the region. GB marine hydrodynamics and meteorological characteristics are briefly described in Sects. 2.1 and 2.2, respectively.
2.1 Hydrodynamic Conditions
Kjerfve et al. (1997) described the GB water circulation as a combination of gravitational circulation and residual tidal circulation, modified by prevailing net wind effects. The authors classified the GB as an estuary dominated by tidal influence. Tidal currents are important because they are responsible for the process of water transport and the mixture between the estuary and the ocean (Miyao and Harari 1989). This type of current is also influenced by the wind through momentum transfer once sufficient wind speed is attained. GB has a pattern of unequal tidal currents, presenting flood currents that are faster than ebb currents (Kjerfve et al. 1997). The most intense velocities are associated with currents aligned with the main navigation channel. Bérgamo (2006) concluded that the tidal currents dominate marine circulation inside and, to some extent, outside the GB estuary.
2.2 Meteorological Conditions
The GB area features a warm, rainy climate in the summer and a cold, dry climate in the winter (Dereczynski et al. 2013). The wind regime over GB is influenced by meteorological processes at different spatial and temporal scales, such as the South Atlantic Subtropical High, cold fronts, and extratropical cyclones, and the local circulation is modulated by sea/land breeze (Pimentel et al. 2014).
Surface wind data from a weather station located at the Santos Dumont Airport (SBRJ) presents a clear pattern in the north-south direction, whereas data from a weather station located at the Antonio Carlos Jobim International Airport (SBGL) in the middle of the bay shows that the wind has a southeast-east pattern (Pimentel et al. 2014).
3 Methodology
In this section, a general overview of the adopted system is presented, and brief information about the computational models, datasets and the analysis are also provided.
To verify the performance of the forecasts produced by this system, hindcast runs were performed. Meteorological and oceanographic data collected by fixed stations and predicted tides for different tidal stations located at GB are used in this paper to evaluate the model results. A similar methodology was used in Blain et al. (2012).
3.1 System Overview
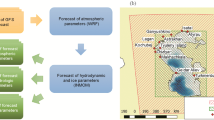
The first stage of this system corresponds to the initial and boundary conditions downloaded from the Global Forecast System (GFS), which are used as input to the atmospheric model, and from Copernicus Marine Environment Monitoring Service (CMEMS), which are used in the ocean model. After this stage, the acquired initial and boundary conditions are interpolated for use in the models. In the next stage, the atmospheric model is executed, and after the integration, the 10-m wind fields and net heat flux at the surface are used as boundary conditions for the following ocean model integration.
Both models are executed daily to yield 72-h prognostics using a three nested grid scheme. The prognostics of the wind fields, sea surface levels and surface current fields are updated daily and are made available on a website. Additionally, to produce more reliable results from the system, observational data are also used to evaluate the model results.
3.2 Atmospheric Model
The atmospheric model used in this study is the Weather Research and Forecasting (WRF) model, which is widely used by the scientific community; its details can be found in Skamarock et al. (2008). The model was configured with three online nested grids, each using a time step of 120 s and 28 vertical levels. The forecast range is 96 h, and the results are generated at 1-h intervals; however, only 72 h are available on the Nautical Strategy Project website. The coarser grid domain covers the South, Middle East and part of the Northeast Brazilian territory. This domain is configured with 100 × 118 grid cells with a horizontal resolution of 27 km. The intermediary domain covers the entire Rio de Janeiro State and part of the Minas Gerais and São Paulo States. This grid is configured with 61 × 58 cells with a horizontal resolution of 9 km. The finest grid domain is centered on GB. It was configured with 64 × 70 grid cells with a horizontal resolution of 3 km. The hierarchy of the WRF grids is illustrated in Fig. 2.
Atmospheric and oceanic nested grid domains meshed: D1 corresponds to the coarse resolution of the atmospheric grid domain (27 km), D2 corresponds to the intermediary domain (9 km) and D3 represents the finest domain (3 km). G1 corresponds to the coarse resolution of the oceanic domain (1 km), G2 corresponds to the intermediary domain (0.2 km) and G3 represents the finest domain (0.1 km).
The Global Forecast System (GFS) results from the 0000 UTC run, with a 0.5º horizontal resolution and a 3-h temporal resolution obtained from the NCEP/NOAA ftp server. These results are used as the initial and boundary conditions for the WRF coarse domain. The intermediate domain used boundary conditions from the coarse domain, and the smallest nested domain used boundary conditions from the intermediate domain. To verify the performance of the atmospheric system, a hindcast was performed for the period of July 2014 to May 2015, and it was used for the analyses presented in the following sections.
3.3 Ocean Model
The ocean model used to simulate the GB hydrodynamics is the Regional Ocean Modelling System (ROMS) (Shchepetkin and McWilliams 2005). ROMS is a free-surface numerical model widely used by the scientific community and has been applied in several studies using different spatial and temporal scales. The model solves the Navier-Stokes equations with hydrostatic and Boussinesq approximations using finite-difference methods. The primitive equations are solved in the horizontal direction in an orthogonal curvilinear coordinate system discretized with an Arakawa-C grid (Shchepetkin and McWilliams 2005; Haidvogel et al. 2008). In the vertical direction, the model uses a terrain-following coordinate system, denoted as S-coordinates that behave as equally spaced sigma-coordinates in shallow regions and as geopotential coordinates in deep regions (Song and Haidvogel 1994).
ROMS was configured in baroclinic mode with three numerical grids using offline nesting (G1, G2 and G3), all with 20 vertical levels (Fig. 2). The bottom topography used in all of the grids was generated using digitalized nautical charts provided by the Brazilian Navy, merged with the bathymetry from ETOPO 2 (National Geophysical Data Center 2006) used for the oceanic region. It was applied a space filter on the generated bathymetry field in order to avoid hydrodynamics inconsistencies during the numerical integration.
The first domain (G1) includes the oceanic region adjacent to Rio de Janeiro State and has a horizontal resolution of 1 km. The initial and boundary conditions for surface displacement, currents and tracers are generated daily using global forecasts from CMEMS (MyOcean 2016). The open boundaries are also forced by astronomical tidal heights and currents derived from the global tide model from TPXO7.2 (Egbert et al. 1994). The second grid (G2) covers the entire GB and near marine coastal area, with a horizontal resolution of 200 m. The third grid (G3) includes the region of GB where the most important nautical activities were performed during the Olympic Games, with a 100-m resolution. The initial conditions for G2 and G3 are extracted and interpolated from the G1 and G2 results, respectively. G2 open boundaries are forced by the prognostic results obtained from the G1, and the lateral conditions for G3 are obtained from the G2 results. The lateral boundary conditions included Chapman for the free surface (Chapman 1985), Flather for the 2D momentum (Flather 1976), and Radiation for the 3D momentum and tracers (Marchesiello et al. 2001).
At the surface, the three oceanic models are forced by the hourly prognostic fields generated by the WRF (previously described), including the wind stress and the net heat flux at the surface. These atmospheric prognostic fields are extracted from the highest resolution WRF grid as a subset. In the operational system, the ROMS simulation is executed daily with a 24-h spin-up period to provide predictions for the following 72 h. In the present paper, a hindcast was performed to obtain results regarding daily oceanic forecasts for the period of September 15 to October 2, 2014. The results from the atmospheric and oceanic models were evaluated using in situ data, as described in the next section.
3.4 Available Data
To evaluate the WRF forecasts, Meteorological Aerodrome Report (METAR) data were used from SBGL and SBRJ stations from July 2014 to May 2015. These fields were selected due to their location near GB (Fig. 1). The wind direction and intensity were extracted from METAR raw data and were decomposed into zonal (u) and meridional (v) vectoral components to compare with the model results. A total of 5,274 observations were used from SBRJ, and 7,128 observations were used from SBGL. During the whole period, SBRJ data between 0300 UTC and 0800 UTC were not available. Also, there was a total of 6 days of missing data for SBRJ.
The oceanographic data used to evaluate the ocean model forecast skill consisted of current profiles and sea surface height data acquired from an Acoustic Doppler current profiler (ADCP) sensor situated near the GB connection with the open ocean at 22.92º S and 43.15º W (Fig. 1), named Laje Station. The ADCP was deployed at a depth of 27 m. The measured data used in this study were the direction and magnitude of the ocean current and pressure converted into depth. The dataset is composed of time series records for the period between September 14 and October 2, 2014. The data were measured at 10-min intervals; however, the data were subsampled, and a 1-h interval was used in the performed analysis. A 48-h high-pass filter and a 6-h low-pass filter were applied to the time series of ADCP data and the modeled results to maintain the tidal oscillation as the main forcing. The spatial variability of the tidal wave representation by the ocean model was also evaluated using the tidal time series predicted for the same period of analysis using sets of harmonic constants from four tidal stations (Fig. 1).
3.5 Performance Assessments
Comparison of the Meteorological Data and Model Results
To evaluate the WRF predictions, statistical indices were used, including a bias, which is commonly used to evaluate model tendencies to over or underestimate wind speed and the root mean square error (RMSE), which demonstrates numerical accuracy. The advantage of these metrics is given by the presentation of error values in the same dimensions as the variable analyzed. The bias and RMSE were calculated using the difference between the atmospheric model result and the observation (model results minus observation). Several articles can be found in the literature in which these statistical indices were used to perform a comparison between the WRF results and observed wind data (Jiménez and Dudhia 2012; Jiménez et al. 2013).
For RMSE, near-zero values indicate better model performance; however, for the bias, also known as systematic error, null values do not necessarily correspond to greater forecast accuracy, because positive and negative errors cancel each other. The dimensionless Pearson linear correlation (COR), which varies from −1 to 1, was also calculated. If the index is equal to 1 (−1), then a perfect positive (negative) correlation between the two variables exists. If this index is null, then the predicted and observed values have no linear relationship. However, one cannot rule out the existence of nonlinear dependencies between the variables with this metric. Thus, from the statistical metrics, one can determine how many days in advance the best prediction will be obtained. To qualitatively evaluate the model, wind roses were generated for observed values and predicted data. Only wind roses of observed data and WRF results for the first 24 h are shown because the 48-, 72- and 96-h results were very similar.
Comparison of the Oceanographic Data and Model Results
To evaluate the skill of the ocean model, hindcast results of G3 were compared to in situ data collected by the ADCP. The time series average (mean) and standard deviation (SD) were used to perform a global assessment of the errors. The central frequency (CF) was computed as the percentage of errors within the following limits. The acceptable error limits used in the present work for the water level displacement and current speed are 10 cm and 0.03 m/s, respectively, and these values were chosen based on the observed levels and speed. The current direction was not considered in this evaluation.
The RMSE, the refined index of agreement (RIA) (Willmott et al. 2012) and COR between model results and observations were calculated. The RIA varies from −1 to 1 and is based in the central tendency of the model-prediction errors and describes the relative co variability of observations and the prediction errors. Positive RIA indicates small model errors in relation to the variance of the observational data, and when the index is equal to 1, a perfect match is observed between predictions and observations. If this index is null the prediction error is twice the sum of observed deviations. Negative RIA values represent poor estimates according as they get close to −1. Nevertheless, RIA values equal to −1 may also mean that little variability is presented in the observed data (Willmott et al. 2012).
These metrics were applied to the ADCP data and model results obtained for G2 model. The RMSE, RIA and COR indices were also computed for the water level time series of the four tidal stations (described above) using local tidal harmonic constants. The complete set of analysis is presented in the next section.
4 Results and Discussion
4.1 Analysis of the Atmospheric Model Results
An analysis of the Table 1 shows that the RMSE increases and COR decreases with time, except for the meridional component RMSE. Furthermore, bias analysis demonstrates that in forecasts with horizons longer than 24 h, the wind speed is overestimated. These results suggest that the forecasts made for the first day exhibit better results compared to other forecasts.
In the wind roses generated with SBGL data (Fig. 3), northeasterly and easterly winds are shown more frequently in the model results than in the observational data. The opposite pattern occurs with southeasterly winds, which occur more frequently than indicated by the model. Furthermore, the percentage of observed calm wind cases is greater than the simulated percentage, which favours wind speed with a positive bias.
Wind roses for (a) observed and (b) predicted winds for the first 24 h of each simulation at Antônio Carlos Jobim International Airport (SBGL - ICAO Code). The SBGL location is shown in Fig. 1.
Wind roses generated for SBGL show a model deficiency in representing the wind’s north-south pattern, which is often observed at SBRJ (not shown). In addition, because synoptic-scale circulation strongly influences the wind directions represented by the model, this circulation also contributes to the predominance of winds from the east quadrant (between the northeast and southeast) in numerical simulations.
The prevailing wind direction and intensity found for both fields correspond with the results of Pimentel et al. (2014), who characterised the land/sea breeze mechanisms in the GB. However, the WRF model results for both aerodromes indicate the strong influence of the synoptic pattern, as the winds from the northeast on the airfield are directly connected with the Subtropical South Atlantic High. This could also be due to topographic misrepresentation because increasing errors are expected in complex terrain regions, as described in Jiménez and Dudhia (2012).
4.2 Analysis of the Ocean Model Results
Sea Surface Height
The sea surface displacements from the mean sea level computed by the ocean model were compared to the level measured by the ADCP at Laje station and the sea level extracted from the harmonic constituents of Armação, Copacabana, Fiscal and Itaipu stations.
The plot of the filtered sea surface height time series measured by the ADCP and the sea level computed by the ocean model is presented in Fig. 4 for a sampling rate of 1 h. The analysis of the observed data reveals the mixed semi-diurnal characteristics of the tides in GB during two neap tide periods and one spring tide period. The same pattern was observed for the water level computed by the ocean model, although some differences were found. The largest differences occur during the spring periods, as the model computes lower amplitudes than those observed, which leads to a better performance during neap tides, as tide amplitudes are expected to be lower. In Fig. 4, it is noted that the model results underestimate the ebb and flood tide heights. Despite these differences in magnitude, the tidal phase signal strongly agrees with the ocean model results, mainly considering the tidal phase.
To quantify the model performance regarding the representation of the sea surface level, some statistical metrics were calculated and are summarized in Tables 2 and 3. In general, the mean and SD of sea level have similar orders of magnitude in all stations, but different absolute sea levels were measured compared to those computed (Table 2). One possible cause to these differences is the river inputs that are not considered in the ocean model, and an average amount of 100 m3/s flow to GB per year (Kjerfve et al. 1997). Considering the sea level predicted at the tidal stations, the ocean model presented high positive correlation values and quadratic errors less than 15 cm (Table 3). The same correspondence is observed considering the refined index of agreement proposed by Willmott et al. (2012). RIA evaluates model performances considering the differences between the model and observed deviations, where values of 1.0 indicate a perfect match. Good agreement indices were obtained in the present work, with the worst index obtained at the Itaipu station. At this station, large average errors were observed. Therefore, this behaviour is expected, as the Itaipu station is located in a region susceptible to the effect of coastal currents and local recirculation.
The next lowest RIA values were observed in Armação and Fiscal Station that also have high RMSE. Both stations are located in the narrow area that borders the main navigation channel at GB (Fig. 1).
Near-Surface Currents
Considering the velocity fields, Fig. 5 shows the currents computed for the G2 model. Ebb and flood occurrences during spring tide periods are represented in this figure, as well as the current speed. Higher flux intensities are observed along the deeper channel in both periods, which is consistent with those described in the literature (Kjerfve et al. 1997).
Several metrics were also used to evaluate the model skill in the representation of GB currents and are presented in Table 3. For this analysis the G3 model results were used. This analysis was performed using the velocities extracted from ADCP measurements (the Laje station) to provide information about the model representativeness of near-surface velocities. The time series for the observed and computed velocities for this layer are shown in Fig. 6.
The mean current speed computed by the G3 ocean model is 0.09 m/s, with a mean direction of 178.51º. Considering the observed currents, the mean speed in the near-surface layer is 0.08 m/s with a mean azimuth of 192.95º (Table 3). Considering the G3 results, the standard deviations computed for magnitude and direction are 0.05 m/s and 105.48º, respectively. This indicates the high variability of the mean flux direction along the integration time, which is expected because the model domain represents a bay mainly dominated by tides. This variability is also observed for currents measured by the ADCP, with the same SD for speed and 107.14º for direction. This similarity between observed and modelled speed and direction can be observed using other statistical metrics, as presented in Table 3.
5 Summary and Conclusions
The Marine and Atmospheric Computational Forecast System developed for nautical sports in GB were demonstrated to be capable of representing the main local atmospheric and oceanic conditions. Considering wind directions, at SBRJ, the observed data presented the North-South axis as its preferential direction, whereas the model indicated a deviation toward the southeast direction. At SBGL, differences were observed with deviations from the observed southeasterly winds ranging from the northeast to southeast directions computed by the WRF. The results from statistics suggests that the forecasts made for the first day exhibit better results compared to other forecasts.
Regarding ocean forecasts, tidal components played an important role in GB circulation. The same pattern in the representation of ebb and flood oscillations was observed for the model results and observations considering both sea level and marine currents. The tidal influence was also observed through the small mean sea level heights and large standard deviations computed by the model and predicted at the four tidal stations. All of the statistical metrics used to evaluate sea level displacement predictions indicated the reasonable performance of the ocean model in terms of the representation of sea surface height. Furthermore, reasonable performances were also observed in terms of ocean current prediction, and the ocean forecasts were representative of local currents. To improve the skill of the present forecast system, some additional developments are planned for future applications. These developments include the analysis of a larger amount of oceanographic and meteorological data and the improvement of spatial resolutions for both models. Additionally, for the atmospheric model, other sets of parameterizations should be tested to construct a WRF ensemble system. For the ocean model, different settings should be tested, and the tidal forcing should be adjusted to better represents the main tidal constituents, in addition to the possible use of data assimilation and the inclusion of water discharges from rivers.
Finally, it is important to emphasize the support that the developed system gave to the Brazilian Sailing Team (BST) during the Rio 2016 Olympic games. The BST conquered one of the best results in olympic games including one gold medal in the 49er class. The sailing coaches and athletes also contribute to the development of the forecast system by means of internal communications about the forecast performance.
References
Bérgamo, A.L.: Características Hidrográficas, da Circulação e dos Transportes de Volume e Sal na Baía de Guanabara (RJ): Variações sazonais e Moduladas pela Maré. [Dissertation]. Universidade de São Paulo, São Paulo (2006)
Blain, C.A., Cambazoglu, M.K., Linzell, R.S., Dresback, K.M., Kolar, R.L.: The predictability of near-coastal currents using a baroclinic unstructured grid model. Ocean Dyn. 62(3), 411–437 (2012)
Chapman, D.C.: Numerical treatment of cross-shelf boundaries in a barotropic coastal ocean model. J. Phys. Oceanogr. 15, 1060–1075 (1985)
Dereczynski, C.P., Luiz Silva, W., Marengo, J.A.: Detection and projections of climate change in Rio de Janeiro. Braz. Am. J. Clim. Change 2, 25–33 (2013). https://doi.org/10.4236/ajcc.2013.21003
Egbert, G.D., Bennett, A.F., Foreman, M.G.G.: TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. 99, 24821–24852 (1994)
Flather, R.A.: A tidal model of the north west European continental shelf. Mem. Soc. R. Sci. Liege. 10, 141–164 (1976)
Golding, B.W., et al.: Forecasting capabilities for the London 2012 Olympics. Bull. Am. Meteorol. Soc. 95(6), 883–896 (2014)
Haidvogel, D.B., et al.: Ocean forecasting in terrain-following coordinates: formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 227(7), 3595–3624 (2008)
Horel, J., et al.: Weather support for the 2002 winter Olympic and Paralympic Games. Bull. Am. Meteorol. Soc. 83(2), 227–240 (2002)
Jiménez, P.A., Dudhia, J.: Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 51(2), 300–316 (2012)
Jiménez, P.A., et al.: An evaluation of WRF’s ability to reproduce the surface wind over complex terrain based on typical circulation patterns. J. Geophys. Res. Atmos. 118(14), 7651–7669 (2013)
Katzfey, J.J., McGregor, J.L.: High-resolution weather predictions for the America’s cup in Auckland: a blend of model forecasts, observations and interpretation. In: Proceedings of the World Weather Research Program Symposium on Nowcasting and Very Short Range Forecasting, Toulouse, France (2005)
Kjerfve, B., Ribeiro, C.H.A., Dias, G.T.M., Filippo, A.M., Da Silva, Q.V.: Oceanographic characteristics of an impacted coastal bay: Baía de Guanabara, Rio de Janeiro. Braz. Cont. Shelf Res. 17(13), 1609–1643 (1997)
Marchesiello, P., McWilliams, J.C., Shcheptkin, A.: Open boundary conditions for long-term integration of regional oceanic models. Ocean Model. 3, 1–20 (2001)
Miyao, S.Y., Harari, J.: Estudo preliminar da maré e das correntes de maré da região estuarina de Cananéia (25S–48°W). Boletim do Instituto Oceanográfico 37(2), 107–123 (1989)
MyOcean: Operational Mercator Global Ocean Analysis and Forecast System. Global Ocean 1/12° Physics Analysis and Forecast Updated Daily (2016). www.myocean.eu
National Geophysical Data Center: 2-minute gridded global relief data (ETOPO2) v2. National Geophysical Data Center, NOAA (2006)
Pimentel, L.C.G., Marton, E., Da Silva, M.S., Jourdan, P.: Caracterização do regime de vento em superfície na Região Metropolitana do Rio de Janeiro. Engenharia Sanitaria e Ambiental 19(2), 121–132 (2014)
Powell, M.D., Rinard, S.K.: Marine forecasting at the 1996 centennial Olympic games. Weather Forecast. 13(3), 764–782 (1998)
Rothfusz, L.P., McLaughlin, M.R., Rinard, S.K.: An overview of NWS weather support for the XXVI Olympiad. Bull. Am. Meteorol. Soc. 79(5), 845–860 (1998)
Shchepetkin, A.F., McWilliams, J.C.: The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9(4), 347–404 (2005). https://doi.org/10.1016/j.ocemod.2004.08.002
Skamarock, W.C., et al.: A description of the advanced research WRF Version 2 (No. NCAR/TN-468+STR). National Center for Atmospheric Research, Boulder, CO, Mesoscale and Microscale Meteorology Div (2008)
Song, Y., Haidvogel, D.: A semi-implicit ocean circulation model using a generalized topography-following coordinate system. J. Comput. Phys. 115(1), 228–244 (1994)
Spark, E., Connor, G.J.: Wind forecasting for the sailing events at the Sydney 2000 Olympic and Paralympic games. Weather Forecast. 19(2), 181–199 (2004)
Vermeersch, W., Alcoforado, M.J.: Wind as a resource for summer nautical recreation. Guincho beach study case. Finisterra 95, 105–122 (2013)
Willmott, C.J., Robeson, S.M., Matsuura, K.: A refined index of model performance. Int. J. Climatol. 32, 2088–2094 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Rangel, R.H.O. et al. (2019). Marine and Atmospheric Forecast Computational System for Nautical Sports in Guanabara Bay (Brazil). In: Rodrigues, J., et al. Computational Science – ICCS 2019. ICCS 2019. Lecture Notes in Computer Science(), vol 11539. Springer, Cham. https://doi.org/10.1007/978-3-030-22747-0_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-22747-0_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22746-3
Online ISBN: 978-3-030-22747-0
eBook Packages: Computer ScienceComputer Science (R0)