Abstract
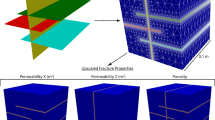
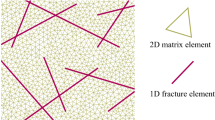
In this paper, we consider a mixed dimensional discrete fracture model with highly conductive fractures. Mathematically the problem is described by a coupled system of equations consisting a d - dimensional equation for flow in porous matrix and a \((d-1)\) - dimensional equation for fracture networks with a specific exchange term for coupling them. For the numerical solution on the fine grid, we construct unstructured mesh that is conforming with fracture surface and use the finite element approximation. Fine grid approximation typically leads to very large systems of equations since it resolves the fracture networks, and therefore some multiscale methods or upscaling methods should be applied. The main contribution of this paper is that we propose a new upscaled model using Non-local multi-continuum (NLMC) method and construct an effective coarse grid approximation. The upscaled model has only one additional coarse degree of freedom (DOF) for each fracture network. We will present results of the numerical simulations using our proposed upscaling method to illustrate its performance.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Akkutlu, I.Y., Efendiev, Y., Vasilyeva, M., Wang, Y.: Multiscale model reduction for shale gas transport in a coupled discrete fracture and dual-continuum porous media. J. Nat. Gas Sci. Engin. 48, 65–76 (2017)
Akkutlu, I.Y., Efendiev, Y., Vasilyeva, M.: Multiscale model reduction for shale gas transport in fractured media. Computat. Geosci. 20(5), 1–21 (2015)
Barenblatt, G.I., Zheltov, I.P., Kochina, I.N.: Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 24(5), 1286–1303 (1960)
Chung, E.T., Efendiev, Y., Leung, W., Vasilyeva, M.: Coupling of multiscale and multi-continuum approaches. GEM-Int. J. Geomath. 8(1), 9–41 (2017)
Chung, E.T., Efendiev, Y., Leung, W.: Constraint energy minimizing generalized multiscale finite element method, arXiv preprint arXiv:1704.03193 (2017)
Chung, E.T., Efendiev, Y., Leung, W., Vasilyeva, M., Wang, Y.: Online adaptive local multiscale model reduction for heterogeneous problems in perforated domains. Appl. Anal. 96(12), 2002–2031 (2017)
Chung, E.T., Efendiev, Y., Leung, W., Wang, Y., Vasilyeva, M.: Non-local multi-continua upscaling for flows in heterogeneous fractured media, arXiv preprint arXiv:1708.08379 (2017)
Chung, E.T., Efendiev, Y., Li, G., Vasilyeva, M.: Generalized multiscale finite element methods for problems in perforated heterogeneous domains. Appl. Anal. 95(10), 2254–2279 (2016)
Efendiev, Y., Galvis, J., Hou, T.: Generalized multiscale finite element methods. J. Comput. Phys. 251, 116–135 (2013)
Efendiev, Y., Hou, T.: Multiscale Finite Element Methods: Theory and Applications. Surveys and Tutorials in the Applied Mathematical Sciences, vol. 4. Springer, New York (2009). https://doi.org/10.1007/978-0-387-09496-0
Jenny, P., Lee, S.H., Tchelepi, H.A.: Adaptive multiscale finite-volume method for multiphase flow and transport in porous media. Multiscale Model. Simul. 3(1), 50–64 (2005)
Tene, M., Al Kobaisi, M.S., Hajibeygi, H.: Algebraic multiscale solver for flow in heterogeneous fractured porous media. In: SPE Reservoir Simulation Symposium, Society of Petroleum Engineers (2015)
Vasilyeva, M., Stalnov, D.: A generalized multiscale finite element method for thermoelasticity problems. In: Dimov, I., Faragó, I., Vulkov, L. (eds.) NAA 2016. LNCS, pp. 713–720. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-319-57099-0_82
Warren, J.E., Root, P.J., et al.: The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 3(03), 245–255 (1963)
D’Angelo, C., Quarteroni, A.: On the coupling of 1D and 3D diffusion-reaction equations: application to tissue perfusion problems. Math. Models Methods Appl. Sci. 18(08), 1481–1504 (2008)
Acknowledgements
MV’s work is supported by the grant of the Russian Scientific Found N17-71-20055. YE’s is supported by the mega-grant of the Russian Federation Government (N 14.Y26.31.0013). EC’s work is partially supported by Hong Kong RGC General Research Fund (Project 14317516) and CUHK Direct Grant for Research 2016-17
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Vasilyeva, M., Chung, E.T., Efendiev, Y., Leung, W.T., Wang, Y. (2019). Upscaled Model for Mixed Dimensional Coupled Flow Problem in Fractured Porous Media Using Non-local Multicontinuum (NLMC) Method. In: Dimov, I., Faragó, I., Vulkov, L. (eds) Finite Difference Methods. Theory and Applications. FDM 2018. Lecture Notes in Computer Science(), vol 11386. Springer, Cham. https://doi.org/10.1007/978-3-030-11539-5_71
Download citation
DOI: https://doi.org/10.1007/978-3-030-11539-5_71
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-11538-8
Online ISBN: 978-3-030-11539-5
eBook Packages: Computer ScienceComputer Science (R0)