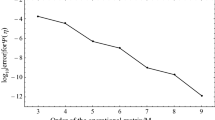
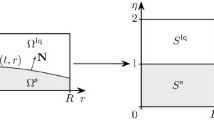
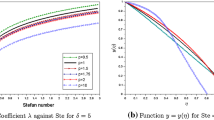
Abstract
The paper presents practically unconditionally stable procedure for numerical study of phase transition in multi-component alloys. The algorithm is based on a conservative fully implicit finite-volume scheme and coupled solution of the governing equations of heat and mass transfer with respect to the vector of all unknowns. The proposed method is implemented for computer simulation of phase changes in a ternary alloy under industrially relevant conditions.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Small, M.B., Ghez, R.: Growth and dissolution kinetics of III-V heterostructures formed by LPE. J. Appl. Phys. 50, 5322 (1979)
Small, M.B., Ghez, R.: Growth and dissolution kinetics of III-V heterostructures formed by LPE. II. Comparison between thermodynamic and kinetic models. J. Appl. Phys. 51, 1589 (1980)
Kimura, M., Qin, Z., Dost, S.: A solid-liquid diffusion model for growth and dissolution of ternary alloys by liquid phase epitaxy. J. Crystal Growth 158, 231–240 (1996)
Dost, S., Lent, B.: Single Crystal Growth of Semiconductors from Metallic Solutions. Elsevier, Amsterdam (2007)
Shcheritsa, O.V., Mazhorova, O.S., Denisov, I.A., Popov, Y.P., Elyutin, A.V.: Numerical study for diffusion processes in dissolution and growth of \({\rm Cd}_x{\rm Hg}_{1-x}{\rm Te}/{\rm CdTe}\) heterostructures formed by LPE. Part I. Isothermal conditions. J. Crystal Growth 290, 350–356 (2006)
Gusev, A.O., Shcheritsa, O.V., Mazhorova, O.S.: Numerical study of ternary alloy crystallization in the cylindrical ampule. Keldysh Institute of Applied Mathematics, Preprint 215 (2016)
Shcheritsa, O.V., Gusev, A.O., Mazhorova, O.S.: On solution to phase transition problem in multicomponent alloy in the cylindrical ampule. Herald Bauman Moscow State Tech. Univ. Nat. Sci. 5, 118–138 (2017)
Bakirova, O.I.: Numerical simulation of zone melting processes on the basis of the solution of the problem of phase transition to binary systems. Mathematical modeling. Producing of crystals and semiconductor structures, pp. 142–158. Moscow, Nauka Publisher (1986). [publication in Russian]
Landau, H.G.: Heat conduction in a melting solid. J. Appl. Math. 8, 81–94 (1950)
Illingworth, T.C., Golosnoy, I.O.: Numerical solutions of diffusion controlled moving boundary problems which conserve solute. J. Comput. Phys. 209, 207–225 (2005)
Mazhorova, O.S., Popov, Y.P., Shcheritsa, O.V.: Conservative scheme for the thermodiffusion Stefan problem. Differ. Equ. 49(7), 869–882 (2013)
Acknowledgments
The study was supported by the Russian Foundation for Basic Research under grant 18-01-00436.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Gusev, A., Mazhorova, O., Shcheritsa, O. (2019). Conservative Finite-Difference Algorithm for the Thermodiffusion Stefan Problem. In: Dimov, I., Faragó, I., Vulkov, L. (eds) Finite Difference Methods. Theory and Applications. FDM 2018. Lecture Notes in Computer Science(), vol 11386. Springer, Cham. https://doi.org/10.1007/978-3-030-11539-5_29
Download citation
DOI: https://doi.org/10.1007/978-3-030-11539-5_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-11538-8
Online ISBN: 978-3-030-11539-5
eBook Packages: Computer ScienceComputer Science (R0)