The Error Analysis of Finite Difference Approximation for a System of Singularly Perturbed Semilinear Reaction-Diffusion Equations with Discontinuous Source Term | SpringerLink
Skip to main content
Springer Nature Link
Log in

The Error Analysis of Finite Difference Approximation for a System of Singularly Perturbed Semilinear Reaction-Diffusion Equations with Discontinuous Source Term

  • Conference paper
  • First Online:
Finite Difference Methods. Theory and Applications (FDM 2018)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 11386))

Included in the following conference series:

Abstract

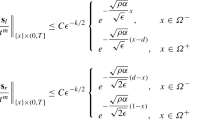
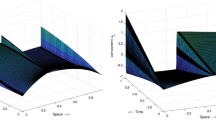
We consider a coupled system of two singularly perturbed semilinear reaction-diffusion equations with a discontinuous source term. The leading term in each equation is multiplied by a small positive parameter, but these parameters have different order of magnitude. The solution of these system of equations have overlapping and interacting boundary and interior layers. Based on the discrete Green’s function theory, the properties of the discretized operator are established. The error estimates are derived in the maximum norm for a central difference scheme on layer-adapted meshes, and the method is proved to be almost second order uniformly convergent independently of both the perturbation parameters. Numerical results validate the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 5719
Price includes VAT (Japan)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 7149
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Andreev, V.B.: On the uniform convergence of a classical difference scheme on a nonuniform mesh for the one-dimensional singularly perturbed reaction-diffusion equation. Comput. Math. Phys. 44, 449–464 (2001)

    Google Scholar 

  2. Boglaev, I., Pack, S.: A uniformly convergent method for a singularly perturbed semilinear reaction-diffusion problem with discontinuous data. Appl. Math. Comput. 182, 244–257 (2006)

    MathSciNet  MATH  Google Scholar 

  3. Farrell, P.A., O’Riordan, E., Shishkin, G.I.: A class of singularly perturbed semilinear differential equations with interior layers. Math. Comput. 74, 1759–1776 (2005)

    Article  MathSciNet  Google Scholar 

  4. Gracia, J.L., Lisbona, F., Madaune-Tort, M., O’Riordan, E.: A system of singularly perturbed semilinear equations. In: Hegarty, A., Kopteva, N., O’Riordan, E., Stynes, M. (eds.) BAIL 2008 - Boundary and Interior Layers. LNCSE, vol. 69, pp. 163–172. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00605-0_12

    Chapter  Google Scholar 

  5. Linß, T., Madden, N.: Layer-adapted meshes for a system of coupled singularly perturbed reaction-diffusion problems. IMA J. Numer. Anal. 29, 109–125 (2009)

    Article  MathSciNet  Google Scholar 

  6. Rao, S.C.S., Chawla, S.: Interior layers in coupled system of two singularly perturbed reaction-diffusion equations with discontinuous source term. In: Dimov, I., Faragó, I., Vulkov, L. (eds.) NAA 2012. LNCS, vol. 8236, pp. 445–453. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-41515-9_50

    Chapter  Google Scholar 

  7. Rao, S.C.S., Chawla, S.: Second order uniformly convergent numerical method for a coupled system of singularly perturbed reaction-diffusion problems with discontinuous source term. In: Knobloch, P. (ed.) BAIL 2014. LNCSE, vol. 108, pp. 233–244. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25727-3_18

    Chapter  Google Scholar 

  8. Chandra Sekhara Rao, S., Chawla, S.: Numerical solution for a coupled system of singularly perturbed initial value problems with discontinuous source term. In: Agrawal, P., Mohapatra, R., Singh, U., Srivastava, H. (eds.) Mathematical Analysis and its Applications. Springer Proceedings in Mathematics & Statistics, vol. 143, pp. 753–764. Springer, New Delhi (2015). https://doi.org/10.1007/978-81-322-2485-3_60

    Chapter  Google Scholar 

  9. Rao, S.C.S., Chawla, S.: Numerical solution of singularly perturbed linear parabolic system with discontinuous source term. Appl. Numer. Math. 127, 249–265 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Delhi, Hauz Khas, New Delhi, 110 016, India

    S. Chandra Sekhara Rao & Sheetal Chawla

Authors
  1. S. Chandra Sekhara Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sheetal Chawla
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Chandra Sekhara Rao .

Editor information

Editors and Affiliations

  1. IICT, Bulgarian Academy of Sciences, Sofia, Bulgaria

    Ivan Dimov

  2. Eötvös Loránd University, Budapest, Hungary

    István Faragó

  3. University of Rousse, Rousse, Bulgaria

    Lubin Vulkov

Rights and permissions

Reprints and permissions

Copyright information

© 2019 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Rao, S.C.S., Chawla, S. (2019). The Error Analysis of Finite Difference Approximation for a System of Singularly Perturbed Semilinear Reaction-Diffusion Equations with Discontinuous Source Term. In: Dimov, I., Faragó, I., Vulkov, L. (eds) Finite Difference Methods. Theory and Applications. FDM 2018. Lecture Notes in Computer Science(), vol 11386. Springer, Cham. https://doi.org/10.1007/978-3-030-11539-5_18

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-11539-5_18

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-11538-8

  • Online ISBN: 978-3-030-11539-5

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation