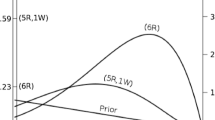
Abstract
The nature of human behavior makes Bayesian methods particularly well-suited for its automated analysis. It is complex, highly variable, frequently inconsistent and is often the consequence of thought processes that we know not of. Advanced modeling techniques that specifically take uncertainty into account are therefore highly desirable. If it were not for the associated computational cost, whether real or perceived, fully Bayesian methods would probably be dominating the field. It can therefore be expected that, as computational power becomes ever more easily and cheaply available, we will see a growing trend towards the wide use of these methods. This chapter introduces the basics of Bayesian methods, and focuses specifically on two major techniques which have received increasing attention in recent years, thanks to their flexibility, ease of use and computational tractability: Dirichlet processes and Gaussian processes.
This chapter introduces the basics of Bayesian methods, and focuses specifically on two major techniques which have received increasing attention in recent years, thanks to their flexibility, ease of use and computational tractability: Dirichlet processes and Gaussian processes.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
For the remainder of this chapter, we handle the convention that vectors are denoted by lowercase bold letters (a,θ,…), while matrices are denoted by uppercase bold letters (A,Σ,…).
- 2.
That is, the prior probability distribution that we had defined over the parameter values. In Bayesian statistics, probabilities are seen as a measure of our belief in the possible values of a variable.
- 3.
With infinite amounts of training data, the prior vanishes and both ML and MAP converge to the same solution.
- 4.
We may nevertheless not be certain which cluster a data point belongs to, so that neither the prior nor the posterior probability that a given data point belongs to a given cluster need to be zero or one.
- 5.
For the purpose of this explanation, we will consider functions of a single, scalar variable, but the concept easily extends to multiple dimensions.
- 6.
To be more formally exact, it is defines the distribution over any finite subset of the variables in that vector to be Gaussian.
References
Adams, R., Ghahramani, Z., Jordan, M.: Tree-structured stick breaking processes for hierarchical modeling. In: Neural Information Processing Systems. MIT Press, Vancouver (2009)
Arulampalam, M.S., Maskell, S., Gordon, N., Clapp, T., Sci, D., Organ, T., Adelaide, S.A.: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 50(2), 174–188 (2002). See also IEEE Transactions on Acoustics, Speech, and Signal Processing
Bergmann, K., Kopp, S.: Modeling the production of coverbal iconic gestures by learning bayesian decision networks. Appl. Artif. Intell. 24(6), 530–551 (2010)
Bishop, C.M.: Pattern Recognition and Machine Learning, 1st edn. Springer, Berlin (2007)
Blei, D.M., Jordan, M.I.: Variational inference for Dirichlet process mixtures. Bayesian Anal. 1(1), 121–144 (2006)
Blei, D.M., Ng, A.Y., Jordan, M.I.: Latent Dirichlet allocation. J. Mach. Learn. Res. 3, 993–1022 (2003)
Cheng, Z., Qin, L., Huang, Q., Jiang, S., Tian, Q.: Group activity recognition by Gaussian process estimation. In: Proceedings of the International Conference on Pattern Recognition, pp. 3228–3231 (2010)
Clamann, H.P.: Statistical analysis of motor unit firing patterns in a human skeletal muscle. Biophys. J. 9(10), 1233–1251 (1969)
Cressie, N.A.C.: Statistics for Spatial Data. Wiley Series in Probability and Statistics. Wiley-Interscience, New York (1993). Rev sub edition
Ek, C.H., Torr, P.H., Lawrence, N.D.: Gaussian process latent variable models for human pose estimation. In: Proceedings of the 2007 Conference on Machine Learning for Multimodal Interfaces (2007)
Ek, C.H., Rihan, J., Torr, P.H., Lawrence, N.D.: Ambiguity modeling in latent spaces. In: Machine Learning for Multimodal Interaction. Lecture Notes in Computer Science, vol. 5237, pp. 62–73. Springer, Berlin (2008)
Ferguson, T.S.: A Bayesian analysis of some nonparametric problems. Ann. Stat. 1(2), 209–230 (1973)
Fox, E.B., Sudderth, E.B., Willsky, A.S.: Hierarchical Dirichlet processes for tracking maneuvering targets. In: 10th Int. Conf. on Information Fusion, pp. 1–8 (2007)
Neal, R.M.: Markov chain sampling methods for Dirichlet process mixture models. J. Comput. Graph. Stat. 9(2), 249–265 (2000)
Rasmussen, C.E., Williams, C.K.I.: Gaussian Processes for Machine Learning. MIT Press, Cambridge (2006)
Teh, Y.W., Jordan, M.I., Beal, M.J., Blei, D.M.: Hierarchical Dirichlet processes. J. Am. Stat. Assoc. 101(476), 1566–1581 (2006)
Wang, J.M., Fleet, D.J., Hertzmann, A.: Gaussian process dynamical models for human motion. IEEE Trans. Pattern Anal. Mach. Intell. 30(2), 283–298 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag London Limited
About this chapter
Cite this chapter
Englebienne, G. (2011). Bayesian Methods for the Analysis of Human Behaviour. In: Salah, A., Gevers, T. (eds) Computer Analysis of Human Behavior. Springer, London. https://doi.org/10.1007/978-0-85729-994-9_1
Download citation
DOI: https://doi.org/10.1007/978-0-85729-994-9_1
Publisher Name: Springer, London
Print ISBN: 978-0-85729-993-2
Online ISBN: 978-0-85729-994-9
eBook Packages: Computer ScienceComputer Science (R0)