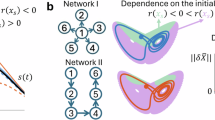
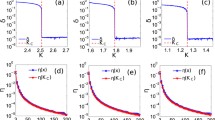
Summary
The structural features of a system significantly affect the attributes and functions of the system. The effect of this phenomenon can be widely observed, from areas such as the WWW to the brains of animals. In the present paper, a method for controlling the behavior of a system by manipulating the structure is examined using a coupled nonlinear oscillator model. We first describe a property of the eigenfrequencies of coupled oscillators and show that convergent transition is possible by connecting oscillators with significantly different eigenfrequencies. Moreover, using the eigenvalues of a graph matrix, we reveal that a combination of distant oscillators can shift the converged state independent of the eigenfrequencies.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
T. McGeer. Passive dynamic walking. The International Journal of Robotics Research, Vol. 9, No. 2, pp. 62–82, 1990.
D.J. Watts and S.H. Strogatz. Collective dynamics of’ small-world’ networks. nature, Vol. 393, pp. 440–442, 1998.
S.H. Strogatz. Exploring complex networks. nature, Vol. 410, pp. 268–276, 2001.
D.S. Callaway, M.E.J. Newman, S.H. Strogatz, and D.J. Watts. Network robustness and fragility: Percolation on random graphs. Physical Review Letters, Vol. 85, No. 25, pp. 5468–5471, 2000.
H. Aonuma, M. Iwasaki, and K. Niwa. Role of no signaling in switching mechanisms in the nervous system of insect. SICE Proc. 2004, pp. 2477–2482, 2004.
D.A. Linkens. Analytical solution of large numbers of mutually coupled nearly sinusoidal oscillators. IEEE Trans. on Circuits and Systems, Vol. CAS-21, No. 2, pp. 294–300, 1974.
D.A. Linkens. Stability of entrainment conditions for a particular form of mutually coupled van der pol oscillators. IEEE Trans. on Circuits and Systems, Vol. CAS-23, No. 2, pp. 113–121, 1976.
Y. Kuramoto. Chemical Oscillations, waves, and Turbulence. Springer, 1984.
A. Jadbabaie, N. Motee, and M. Barahona. On the stability of the kuramoto model of coupled nonlinear oscillators. In the American Control Conference, 2004.
M.G. Earl and S.H. Strogatz. Synchronization in oscillator networks with delayed coupling: A stability criterion. Physical Review E, Vol. 67, p. 036204, 2003.
C.M. Gray, P. Konig, A.K. Engel, and W. Singer. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. nature, Vol. 338, pp. 334–337, 1989.
F.C. Hoppensteadt and E.M. Izhikevich. Oscillatory neurocomputers with dynamic connectivity. Physical Review Letters, Vol. 82, No. 14, pp. 2383–2386, 1999.
H. Haken. Advanced Synergetics. Springer, 1983.
L.M. Pecora and T.L. Carroll. Master stability functions for synchronized coupled systems. Physical Review Letters, Vol. 80, No. 10, p. 2109, 1998.
M. Barahona and L.M. Pecora. Synchronization in small-world systems. Physical Review Letters, Vol. 89, No. 5, pp. 054101-1–054101-4, 2002.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Tokyo
About this paper
Cite this paper
Funato, T., Kurabayashi, D., Nara, M. (2006). Synchronization Control by Structural Modification of Nonlinear Oscillator Network. In: Gini, M., Voyles, R. (eds) Distributed Autonomous Robotic Systems 7. Springer, Tokyo. https://doi.org/10.1007/4-431-35881-1_5
Download citation
DOI: https://doi.org/10.1007/4-431-35881-1_5
Publisher Name: Springer, Tokyo
Print ISBN: 978-4-431-35878-7
Online ISBN: 978-4-431-35881-7
eBook Packages: EngineeringEngineering (R0)