Weaving patterns of lines and line segments in space

Abstract

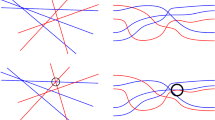
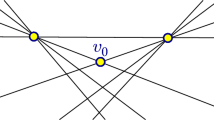
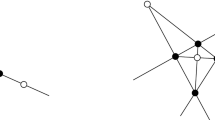
A weaving W is a simple arrangement of lines (or line segments) in the plane together with a binary relation specifying which line is “above” the other. An m by n bipartite weaving consists of m horizontal and n vertical lines or line segments which mutually intersect. A system of lines (or line segments) in 3-space is called a realization of W, if its projection into the plane is W and the relative positions of the lines respect the “above” specifications. An equivalence class of weavings induced by the combinatorial equivalence of the underlying planar arrangement of lines is said to be a weaving pattern. A weaving pattern is realizable if at least one element of the equivalence class has a realization. A weaving (pattern) W is called perfect, if along each line of W, the lines intersecting it are alternately “above” and “below”. We prove that (i) a perfect weaving pattern of n lines is realizable if and only if n≤3, (ii) a perfect m by n bipartite weaving pattern is realizable if and only if min(m, n)≤3, (iii) if n is sufficiently large then almost all weaving patterns of n lines are nonrealizable.

Supported in part by Hungarian NFSR grant 1812, NSF grant CCR-8901484 and the Center for Discrete Mathematics and Theoretical Computer Science (DIMACS), a National Science Foundation Science and Technology Center, under NSF grant STC88-09648.

Supported in part by NSA grant MDA904-89-H-2030, NSF grants DMS-85-01947 and CCR-8901484, and DIMACS.

Supported in part by the ESPRIT II Basic Research Actions Program of the EC under contract no. 3075 (project ALCOM) and DIMACS