Moving regular k-gons in contact

Abstract

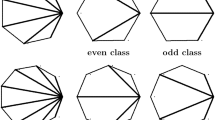
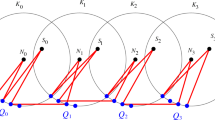
Given m circles in the plane, contacts between them can be specified by a system of quadratic distance equalities. An approximative solution for the trajectories of the circles for a system of one degree of freedom is given, by replacing the circles by translationally moving regular k-gons. The approximation yields trajectories that are piecewise linear. The next linear generation of the m trajectories are found by an incremental algorithm in O(m ²) time. Further, an algorithm is presented which finds the next collision between m k-gons moving on lines at constant speed in time O(k · m ^2−x) for a constant x>0 using linear space. Finally, more practical collision detection algorithms are sketched based on neighborhood information which, however, do not guarantee a nontrivial worst-case time bound.

partially supported by Deutsche Forschungsgemeinschaft (DFG, Mu744/1-1)