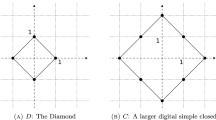
Abstract
As its analogue in the continuous framework, the digital fundamental group represents a major information on the topology of discrete objects. However, the fundamental group is an abstract information and cannot directly be encoded in a computer using its definition. A classical mathematical way to encode a discrete group is to find a presentation of this group. In this paper, we define a presentation for the fundamental group of any subset of a digital surface. This presentation can be computed by an efficient algorithm.
Chapter PDF
Similar content being viewed by others
References
G. Bertrand, Simple points, topological numbers and geodesic neighbourhoods in cubic grids, Pattern Rec. Letters, 15, pp 1003–1011, 1994.
[2] T.J. Fan, G. Medioni, and R. Nevata. Recognising 3d Objects using Surface Descriptions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1111, pp 1140–1157, 1989.
G.T. Herman, Discrete Multidimensional Jordan Surfaces. CVGIP: Graphical Models and Image Processing, 54(6) pp 507–515, November 1992.
T.Y. Kong, A Digital Fundamental Group Computer and Graphics, 13, pp 159–166, 1989.
T.Y. Kong, Polyhedral Analogs of Locally Finite Topological SpacesR.M. Shortteditor, General Topology and Applications: Proceedings of the 1988 North-east Conference, Middletown, CT (USA), Lecture Notes in Pure and Applied Mathematics, 123, pp 153–164, 1990.
A. Lenoir, Fast Estimation of Mean Curvature on the Surface of a 3D Discrete Object, Proceeding of DGCI’97, Lecture Notes in Computer Science1347, pp 175–186, 1997.
R. Malgouyres, Homotopy in 2-dimensional Digital Images, Proceeding of DGCI’97, Lecture Notes in Computer Science1347, pp 213–222, 1997.
R. Malgouyres, Homotopy in 2-dimensional Digital Images, Theoretical Computer Science, to appear.
R. Malgouyres, A. Lenoir, Topology Preservation Within Digital Surfaces, Proceedings of Computer Graphics and Image Processing, Warsaw, May 1998, Machine GRAPHICS & VISION, vol 7, Nos 1/2, pp 417–425, 1998.
J.K. Udupa. Multidimensional digital boundaries. CVGIP: Graphical Models and Image Processing, 56(4), pp 311–323, July 1994.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1999 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Malgouyres, R. (1999). Presentation of the Fundamental Group in Digital Surfaces. In: Bertrand, G., Couprie, M., Perroton, L. (eds) Discrete Geometry for Computer Imagery. DGCI 1999. Lecture Notes in Computer Science, vol 1568. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-49126-0_11
Download citation
DOI: https://doi.org/10.1007/3-540-49126-0_11
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-65685-2
Online ISBN: 978-3-540-49126-2
eBook Packages: Springer Book Archive