Abstract
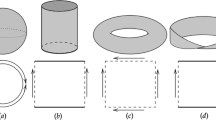
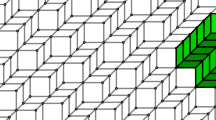
A new method of representing a surface in the 3D space as a single digitally continuous sequence of faces is described. The method is based on topological properties of quasi-manifolds. It is realized as tracing the boundary of a growing set of labeled faces. As the result the surface is encoded as a single sequence of mutually adjacent faces. Each face is encoded by one byte. The code of the surface of a three-dimensional object takes much less memory space then the raster representation of the object. The object may be exactly reconstructed from the code. Surfaces of a genus greater that zero (e.g. that of a torus) may also be encoded by a single continuous sequence. The traversal algorithm recognizes the genus of the surface.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Gordon, D., Udupa, J.K., Fast Surface Tracking in Three-Dimensional Binary Images, CVGIP, v. 45, pp. 196–214, 1989.
Khalimsky, E., Kopperman, R. and Meyer, P.R., Computer Graphics and Connected Topologies on Finite Ordered Sets, Topology and Applications, v. 36, pp. 1–17, 1990.
T. Young Kong, „On Boundaries and Boundary Crack-Codes of Multidimensional Digital Images“, in „Shape in Picture“, Ying-Lie O et. all (Eds.), Springer-Verlag, 1992.
Kovalevsky, V.A., “Finite Topology as Applied to Image Analysis”, Computer Vision, Graphics and Image Processing, v. 46, pp. 141–161, 1989.
Kovalevsky, V.A., “Finite Topology and Image Analysis”, In “Image Mathematics and Image Processing”, P. Hawkes(Ed.), „Advances in Electronics and Electron Physics“, v. 84, pp. 197–259, Academic Press 1992.
Kovalevsky, V.A., “Digital Geometry Based on the Topology of Abstract Cell Complexes”, Proceedings of the Third International Colloquium “Discrete Geometry for Computer Imagery”, pp. 259–284, University of Strasbourg 1993.
Kovalevsky, V.A., „Applications of Digital Straight Segments to Economical Image Encoding“, In: Ahronovitz, E. and Fiorio, C: (eds.), “Discrete Geometry for Computer Imagery”, Proceedings of the 7th International Workshop, DGCI’97, pp. 51–62, Springer 1997.
A. Rosenfeld, T. Young Kong and A.Y. Wu, „Digital Surfaces“, CVGIP GMIP, v. 53, pp. 305–312, 1991.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1999 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Kovalevsky, V. (1999). A Topological Method of Surface Representation. In: Bertrand, G., Couprie, M., Perroton, L. (eds) Discrete Geometry for Computer Imagery. DGCI 1999. Lecture Notes in Computer Science, vol 1568. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-49126-0_10
Download citation
DOI: https://doi.org/10.1007/3-540-49126-0_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-65685-2
Online ISBN: 978-3-540-49126-2
eBook Packages: Springer Book Archive