Abstract
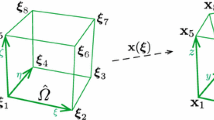
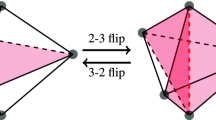
The quality improvement in mesh optimisation techniques that preserve its connectivity are obtained by an iterative process in which each node of the mesh is moved to a new position that minimises a certain objective function. In general, objective functions are derived from some quality measure of the local submesh, that is, the set of tetrahedra connected to the adjustable or free node. Although these objective functions are suitable to improve the quality of a mesh in which there are non inverted elements, they are not when the mesh is tangled. This is due to the fact that usual objective functions are not defined on all ℝ3 and they present several discontinuities and local minima that prevent the use of conventional optimisation procedures. Otherwise, when the mesh is tangled, there are local submeshes for which the free node is out of the feasible region, or this does not exist. In this paper we propose the substitution of objective functions having barriers by modified versions that are defined and regular on all ℝ3. With these modifications, the optimisation process is also directly applicable to meshes with inverted elements, making a previous untangling procedure unnecessary.
Partially supported by MCYT, Spain. Grant contract: REN2001-0925-C03-02/CLI
The authors acknowledge Dr. David Shea for editorial assistance
Chapter PDF
Similar content being viewed by others
References
Bank, R.E., Smith, R.K.: Mesh Smoothing Using a Posteriori Error Estimates. SIAM J. Numer. Anal. 34 (1997) 979–997
Bazaraa, M.S., Sherali, H.D., Shetty, C.M.: Nonlinear Programing: Theory and Algorithms. John Wiley and Sons, Inc., New York, (1993)
Djidjev, H.N.: Force-Directed Methods for Smoothing Unstructured Triangular and Tetrahedral Meshes. Tech. Report, Department of Computer Science, Univ. of Warwick, Coventry, UK, (2000). Available from http://www.andrew.cmu.edu/user
Dompierre, J., Labbé, P., Guibault, F., Camarero, R.: Proposal of Benchmarks for 3D Unstructured Tetrahedral Mesh Optimization. In Proc. 7th International Meshing Roundtable. Sandia National Laboratories (1998) 459–478
Escobar, J.M., Montenegro, R.: Several Aspects of Three-Dimensional Delaunay Triangulation. Adv. Eng. Soft. 27(1/2) (1996) 27–39
Ferragut, L., Montenegro, R., Plaza, A.: Efficient Refinement/Derefinement Algorithm of Nested Meshes to Solve Evolution Problems. Comm. Numer. Meth. Eng. 10 (1994) 403–412
Freitag, L.A., Knupp, P.M.: Tetrahedral Element Shape Optimization Via the Jacobian Determinant and Condition Number. In Proc. of the 8th International Meshing Roundtable. Sandia National Laboratories (1999) 247–258
Freitag, L.A., Jones, M., Plassmann, P.: A Parallel Algorithm for Mesh Smoothing. SIAM J. Sci. Comput. 20 (2000) 2023–2040
Freitag, L.A., Plassmann, P.: Local Optimization-based Simplicial Mesh Untangling and Improvement. Int. J. Numer. Meth. Eng. 49 (2000) 109–125
Freitag, L.A., Knupp, P.M.: Tetrahedral Mesh Improvement via Optimization of the Element Condition Number. Int. J. Numer. Meth. Eng. 53 (2002) 1377–1391
Knupp, P.M.: Algebraic Mesh Quality Metrics. SIAM J. Sci. Comput. 23 (2001) 193–218
Knupp, P.M.: Achieving Finite Element Mesh Quality via Optimization of the Jacobian Matrix Norm and Associated Quantities. Part II-A Frame Work for Volume Mesh Optimization and the Condition Number of the Jacobian Matrix. Int. J. Numer. Meth. Eng. 48 (2000) 1165–1185
Montenegro, R., Montero, G., Escobar, J.M., Rodíguez, E., González-Yuste, J.M.: Tetrahedral Mesh Generation for Environmental Problems over Complex Terrains. In: Sloot, P.M.A., Tan, C.J.K., Dongarra, J.J., Hoekstra, A.G. (eds.): Computational Science-ICCS’2002. Lecture Notes in Computer Science, Vol. 2329. Springer-Verlag, Berlin Heidelberg New York (2002) 335–344
Montenegro, R., Montero, G., Escobar, J.M., Rodríguez, E.: Efficient Strategies for Adaptive 3-D Mesh Generation over Complex Orography. Neural, Parallel & Scientific Computation 10(1) (2002) 57–76
Rodríguez, E., Montero, G., Montenegro, R., Escobar, J.M., González-Yuste, J.M.: Parameter Estimation in a Three-dimensional Wind Field Model Using Genetic Algorithms. In: Sloot, P.M.A., Tan, C.J.K., Dongarra, J.J., Hoekstra, A.G. (eds.): Computational Science-ICCS’2002. Lecture Notes in Computer Science, Vol. 2329. Springer-Verlag, Berlin Heidelberg New York (2002) 950–959
Pain, C.C., Umpleby, A.P., Oliveira, C.R.E. de, Goddard, A.J.H.: Tetrahedral Mesh Optimization for Steady-State and Transient Finite Element Calculations. Comput. Meth. Appl. Mech. Eng. 190 (2001) 3771–3796
Tam, A., Ait-Ali-Yahia, D., Robichaud, M.P., Moore, A., Kozel, V., Habashi, W.G.: Anisotropic Mesh Adaptation for 3-D Flows on Structured and Unstructured Grids. Comput. Meth. Appl. Mech. Eng. 189 (2000) 1205–1230
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Montenegro, R., Escobar, J.M., Rodríguez, E., Montero, G., González-Yuste, J.M. (2003). Improved Objective Functions for Tetrahedral Mesh Optimisation. In: Sloot, P.M.A., Abramson, D., Bogdanov, A.V., Dongarra, J.J., Zomaya, A.Y., Gorbachev, Y.E. (eds) Computational Science — ICCS 2003. ICCS 2003. Lecture Notes in Computer Science, vol 2657. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44860-8_59
Download citation
DOI: https://doi.org/10.1007/3-540-44860-8_59
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-40194-0
Online ISBN: 978-3-540-44860-0
eBook Packages: Springer Book Archive