Abstract
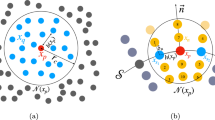
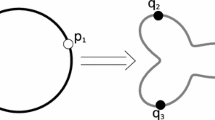
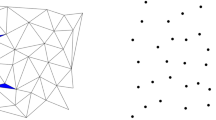
Meshing of surfaces is an ubiquitous problem in many applications of science and engineering. Among different approaches available for meshing surfaces, Delaunay meshing is often favored because of its directional independence and good quality in general. As application varies, so does the input form of the surface to be meshed. We present algorithms to compute Delaunay meshes for various forms of input surfaces. Specifically, we consider surfaces input with (i) point cloud data, (ii) implicit equations, and (iii) polyhedra. These algorithms come with theoretical guarantees and some of them have been successfully implemented. In this talk we detail the algorithms, provide the mathematical reasoning behind their designs, and show the results of some experiments.
Similar content being viewed by others
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dey, T.K. (2006). Delaunay Meshing of Surfaces. In: Asano, T. (eds) Algorithms and Computation. ISAAC 2006. Lecture Notes in Computer Science, vol 4288. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11940128_2
Download citation
DOI: https://doi.org/10.1007/11940128_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-49694-6
Online ISBN: 978-3-540-49696-0
eBook Packages: Computer ScienceComputer Science (R0)