Gridland
Time Limit: 1000MS | | Memory Limit: 10000K |
Total Submissions: 8258 | | Accepted: 4185 |
Description
Background
For years, computer scientists have been trying to find efficient solutions to different computing problems. For some of them efficient algorithms are already available, these are the "easy" problems like sorting, evaluating a polynomial or finding the shortest path in a graph. For the "hard" ones only exponential-time algorithms are known. The traveling-salesman problem belongs to this latter group. Given a set of N towns and roads between these towns, the problem is to compute the shortest path allowing a salesman to visit each of the towns once and only once and return to the starting point.
Problem
The president of Gridland has hired you to design a program that calculates the length of the shortest traveling-salesman tour for the towns in the country. In Gridland, there is one town at each of the points of a rectangular grid. Roads run from every town in the directions North, Northwest, West, Southwest, South, Southeast, East, and Northeast, provided that there is a neighbouring town in that direction. The distance between neighbouring towns in directions North-South or East-West is 1 unit. The length of the roads is measured by the Euclidean distance. For example, Figure 7 shows 2 * 3-Gridland, i.e., a rectangular grid of dimensions 2 by 3. In 2 * 3-Gridland, the shortest tour has length 6.
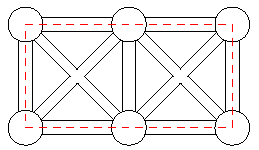
Figure 7: A traveling-salesman tour in 2 ? 3-Gridland.
Input
The first line contains the number of scenarios.
For each scenario, the grid dimensions m and n will be given as two integer numbers in a single line, separated by a single blank, satisfying 1 < m < 50 and 1 < n < 50.
Output
The output for each scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. In the next line, print the length of the shortest traveling-salesman tour rounded to two decimal digits. The output for every scenario ends with a blank line.
Sample Input
22 2 2 3
Sample Output
Scenario #1:4.00 Scenario #2: 6.00
解题思路:
因为要遍历所有节点,而且最后回到起始节点,那所要经过的边的数目就是节点的数目m*n,问题的关键就是考虑m*n条边中有多少个斜边。经过分析可以得出一条规律:当m或n都是偶数时没有斜边;否则会有一条斜边。代码:#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
using namespace std;
int main()
{
int n,m;
int t;
cin>>t;
float dis;
int k=1;
while(t--)
{
cin>>n>>m;
if(n%2==0||m%2==0)
dis=m*n;
else
dis=m*n-1+sqrt(2.0);
printf("Scenario #%d:\n",k++);
printf("%.2f\n",dis);
printf("\n");
}
return 0;
}


















