损失函数大致分为两类：回归（Regression）和分类（Classification）。
回归模型中的三种损失函数包括：
- 均方误差(Mean Square Error, MSE)
- 平均绝对误差（Mean Absolute Error, MAE）
- Huber Loss
均方误差(Mean Square Error, MSE)
指模型预测值
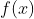
与样本真实值
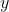
之间距离平方的平均值：
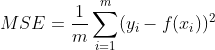
其中
yi和
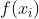
分别表示第
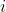
个样本的真实值和预测值，
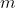
为样本个数。
MSE 曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛，即使固定学习因子，函数也能较快取得最小值。
平方误差有个特性，就是当 yi 与 f(xi) 的差值大于 1 时，会增大其误差；当 yi 与 f(xi) 的差值小于 1 时，会减小其误差。这是由平方的特性决定的。也就是说， MSE 会对误差较大（>1）的情况给予更大的惩罚，对误差较小（<1）的情况给予更小的惩罚。从训练的角度来看，模型会更加偏向于惩罚较大的点，赋予其更大的权重。
如果样本中存在离群点，MSE 会给离群点赋予更高的权重，但是却是以牺牲其他正常数据点的预测效果为代价，这最终会降低模型的整体性能。我们来看一下使用 MSE 解决含有离群点的回归模型。
平均绝对误差（Mean Absolute Error, MAE）
平均绝对误差指的就是模型预测值 f(x) 与样本真实值 y 之间距离的平均值。其公式如下所示：
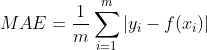
直观上来看，MAE 的曲线呈 V 字型，连续但在 y-f(x)=0 处不可导，计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。
值得一提的是，MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感，更有包容性。因为 MAE 计算的是误差 y-f(x) 的绝对值，无论是 y-f(x)>1 还是 y-f(x)<1，没有平方项的作用，惩罚力度都是一样的，所占权重一样。
Huber Loss
Huber Loss是MSE和MAE的综合，通过一个超参数决定其更偏向于是MSE还是MAE。公式如下：
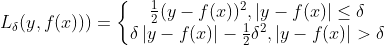\delta \end{matrix}\right." title="L_{\delta }(y,f(x)))=\left\{\begin{matrix} \frac{1}{2}(y-f(x))^{2},\left | y-f(x) \right |\leq \delta \\ \delta\left|y-f(x)\right|-\frac{1}{2}\delta^{2},\left | y-f(x) \right |> \delta \end{matrix}\right." style="width: 385px; visibility: visible;" data-type="block">
当 |y−f(x)| ≤ δ 时，变为 MSE；当 |y−f(x)| > δ 时，则变成类似于 MAE，因此 Huber Loss 同时具备了 MSE 和 MAE 的优点，减小了对离群点的敏感度问题，实现了处处可导的功能。通常通过交叉验证选择超参数
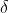
的最佳值。
MSE 的 Loss 下降得最快，MAE 的 Loss 下降得最慢，Huber Loss 下降速度介于 MSE 和 MAE 之间。
在回归任务中，我们还会使用log-cosh loss，它可以保证二阶导数的存在，有些优化算法会用到二阶导数，在xgboost中我们同样需要利用二阶导数；同时，我们还会用到分位数损失，希望能给不确定的度量。
除了log和hinge，在分类任务中，我们还有对比损失（contrastive loss）、softmax cross-entropy loss、中心损失（center loss）等损失函数，它们一般用在神经网络中。
