柯西-黎曼方程(简称C-R方程)是在复分析中用来判定一个复变函数是否可微的充要条件,本文试图用代数和几何两种方法来理解它到底说了什么。
代数证明:
在复变函数领域,f(z)在
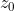
处解析=>f(z)在
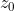
处可导<=>f(z)在
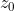
处可微
证明1:
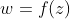
,则在
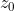
处:
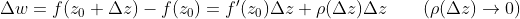
令
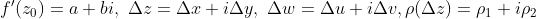
代入上式:
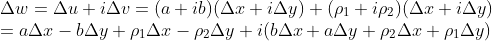
根据复数相等的条件:
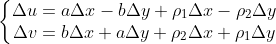
我们希望留下上面的a,b主项,去掉
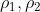
项目,现在来证明:
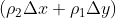
以及
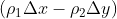
均为无穷小.
由于:
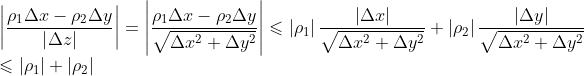
当
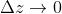
时,
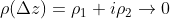
,等价于,当
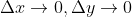
时,
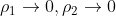
所以,
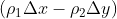
是比
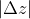
更高阶的无穷小,同理,
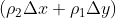
也可以得到这个结论。
所以:
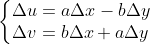
根据二元函数偏导数的性质,可以得到:
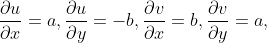
所以,可以推出:
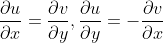
证明2:
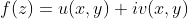
,再 区域D内一点
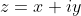
可导,可以得到:
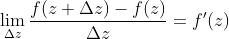
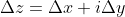
,
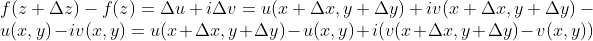
所以:
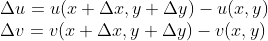
所以:
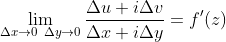
因为
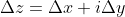
无论按照什么方式趋近于0,上面的式子总是成立,所以这里取两条特殊路径: 第一条:
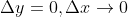
第二条:
路径如下图所示:
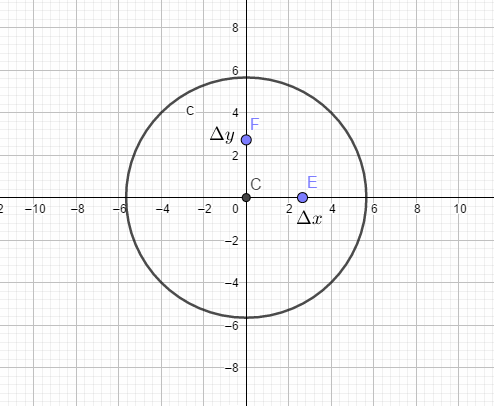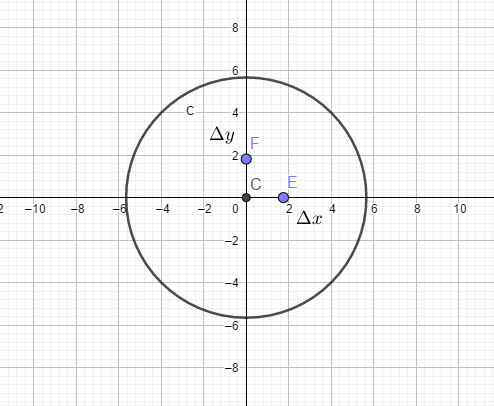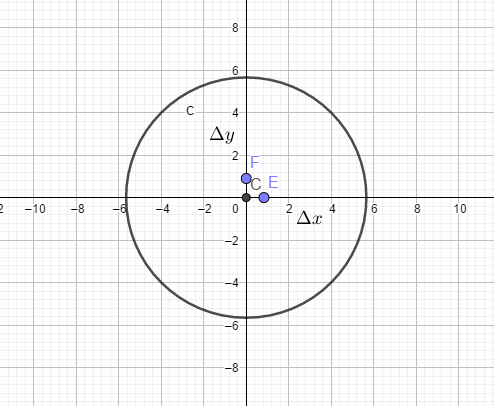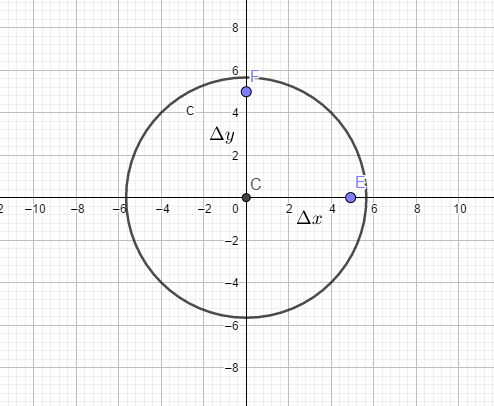
按照路径1:
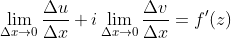
所以,
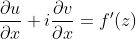
按照路径2:
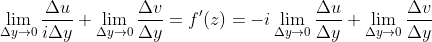
如果函数解析,则两条路径计算得到导数应该是一样的,也就是
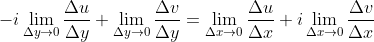
根据复数相等的条件:
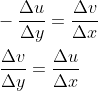
也就是:
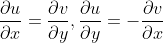
几何证明:
上面的代数证明已经说过了,复变函数的导数如果存在,要求

的方式是任意的,这一点要比实变量的情况复杂的多,对于实变函数来说,导数存在意味着,当点
由左(
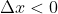
)以及右(
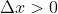
)两个方向趋近x0时,比值
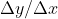
的极限都存在且相等。而复变函数的导数存在性意味着,当点
,沿着连接点
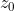
的任意路径趋近于
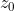
时,比值
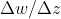
的极限都存在,并且这些极限都相等,可见复变函数的可微条件要比实变函数可微条件要更苛刻一些。
如下图:
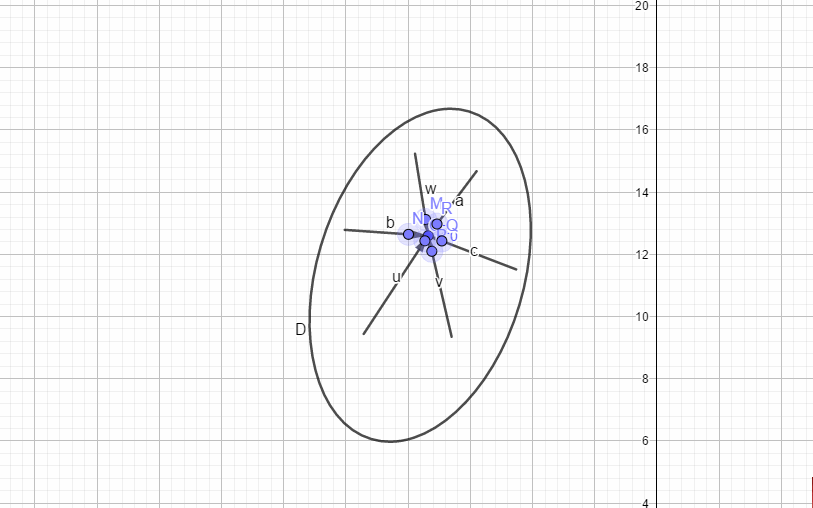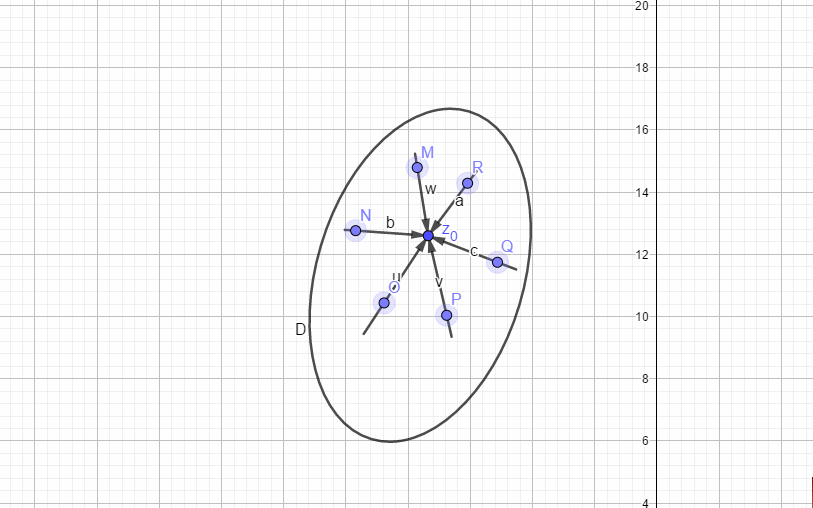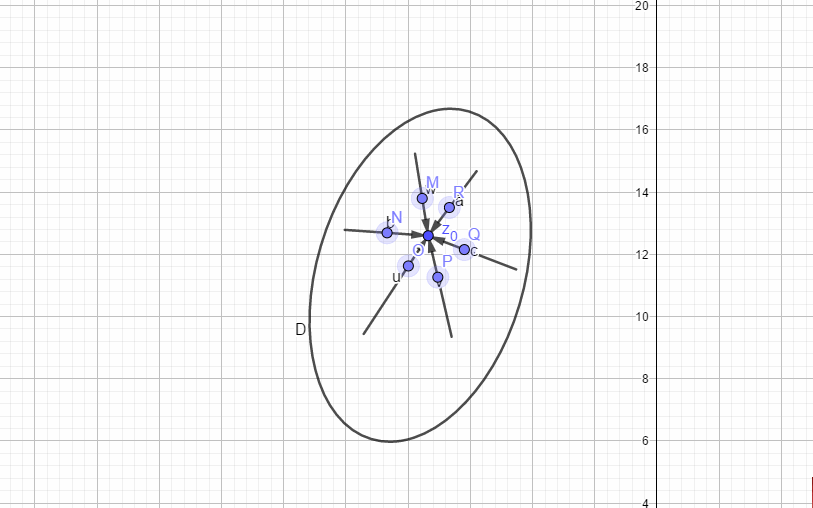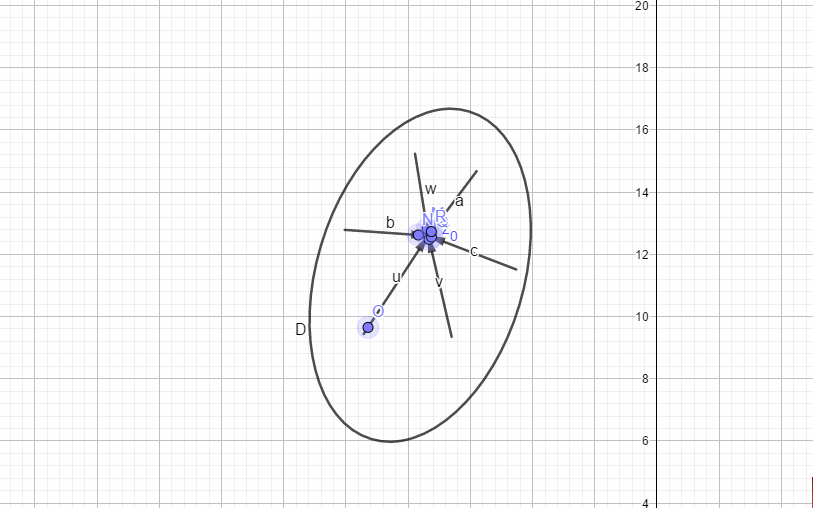
在
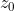
可导,意味着:
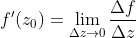
存在,根据复数的运算法则,
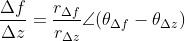
这也意味着沿着任何轨迹接近
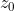
.
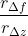
和
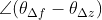
都为固定值,其中
称为伸缩率,
为转动角。
如下图所示:
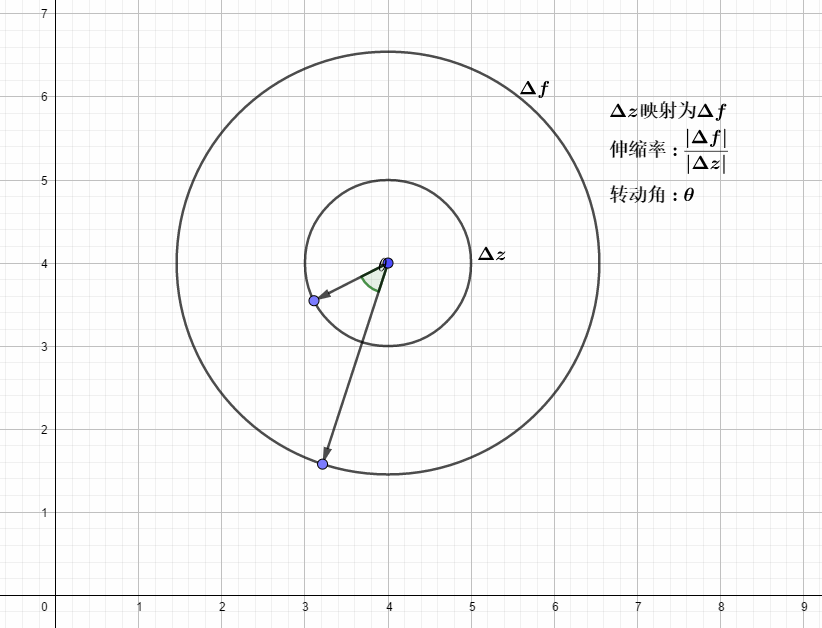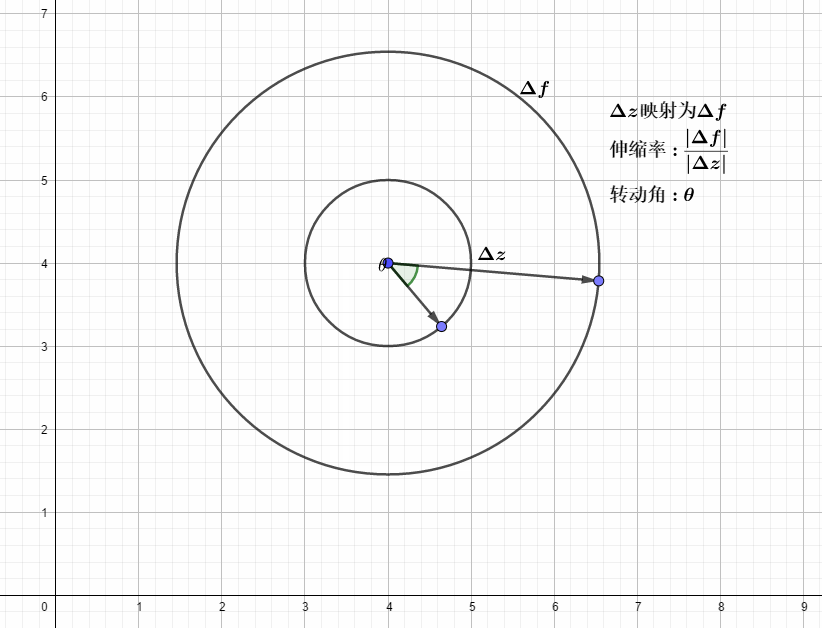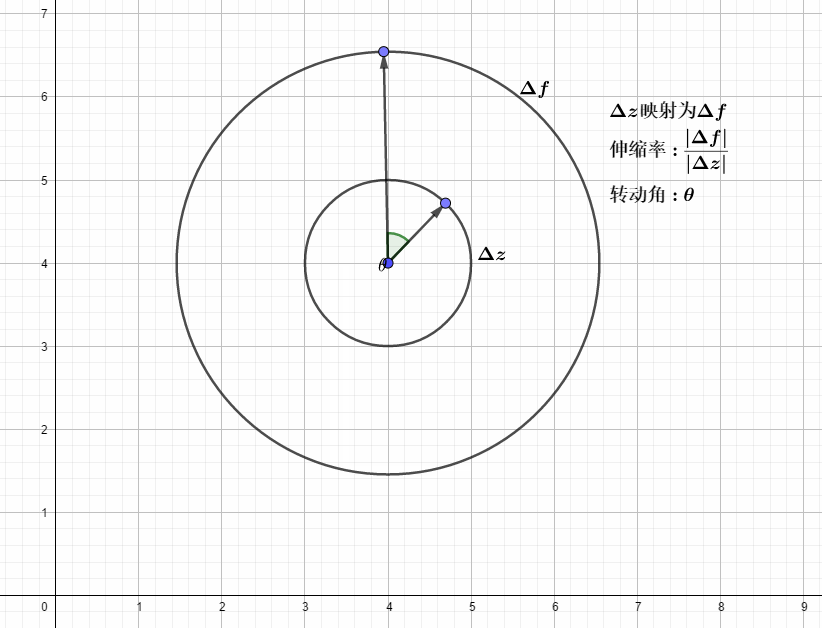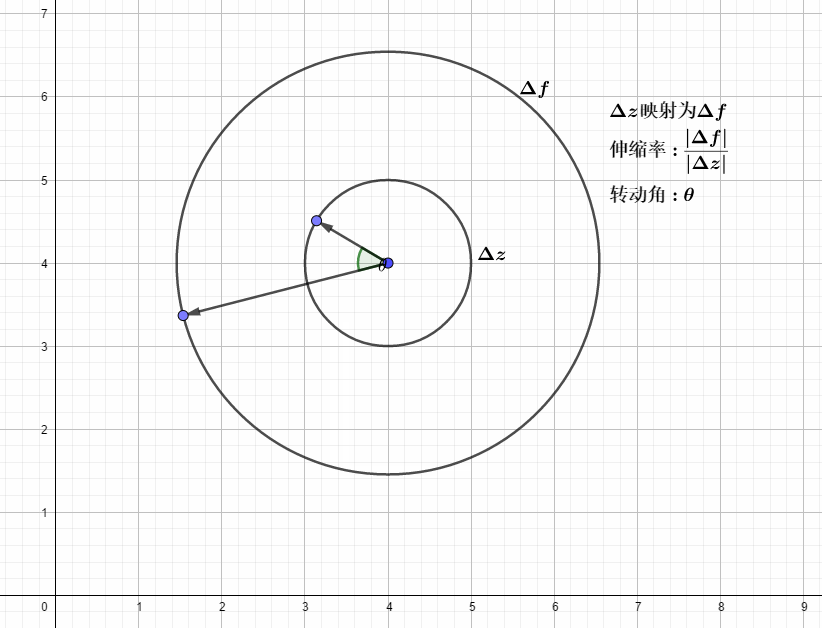
以复变函数
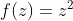
为例,先根据C-R方程判断它的可导性:
令:
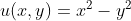
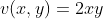
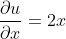
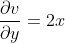
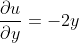
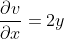
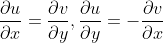
成立。
所以
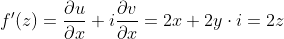
,
或者:
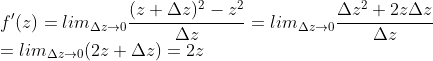
所以
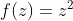
是处处可导的,导数为
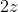
。复变函数
再
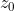
处的导数为
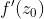
,则沿着不同的路径得到的导数应该均为
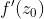
,从多条接近路径中任意选取两条h,g,并且路径h,g之间的夹角为
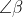
.
可以得到
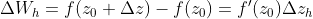
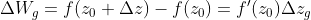
令:
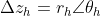
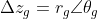
并且
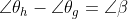
所以
所以,当再h,g线上经过微小的摄动后:w=f(z)在h,g方向上的变化矢量方向为
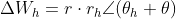
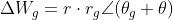
注意到
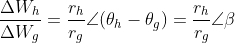
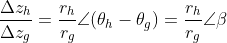
所以微小的摄动经过复函数变换后,得到的方向矢量仍然相差
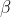
角度,这就是复变解析函数的“保角特性”,这就直观地解释了复变函数解析性能推出保角性,并说明了导数的几何意义。
如下图所示,左边h,g两条路径的夹角和右图两条曲线的夹角必定是相同的。根据这个性质也可以推出C-R方程。
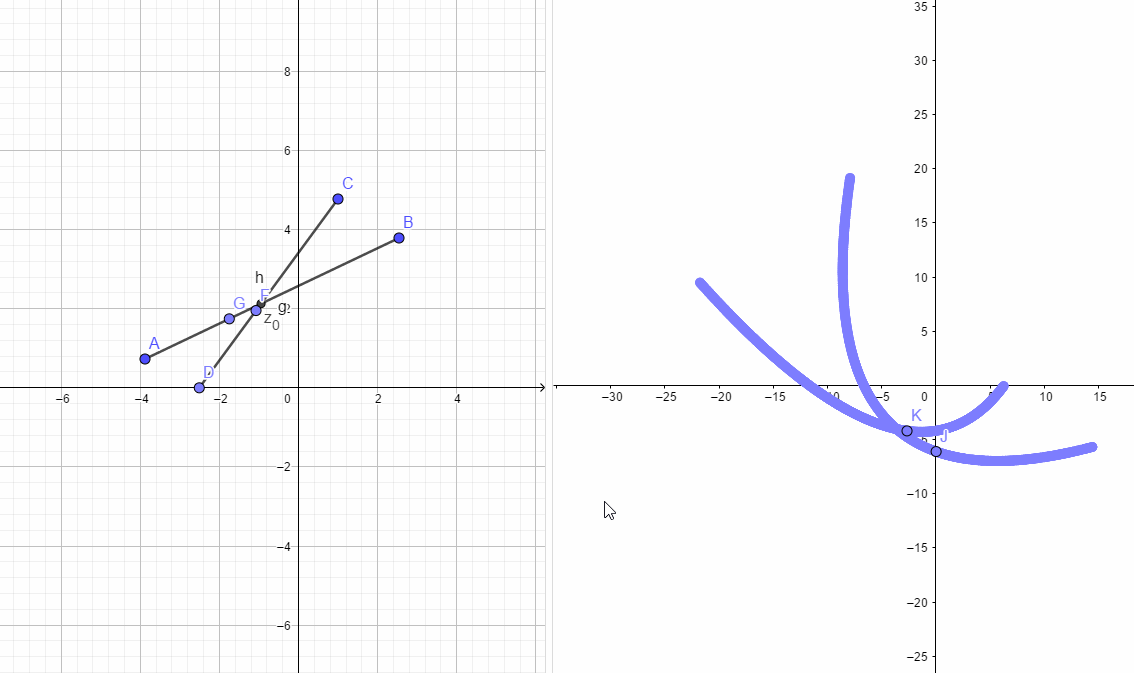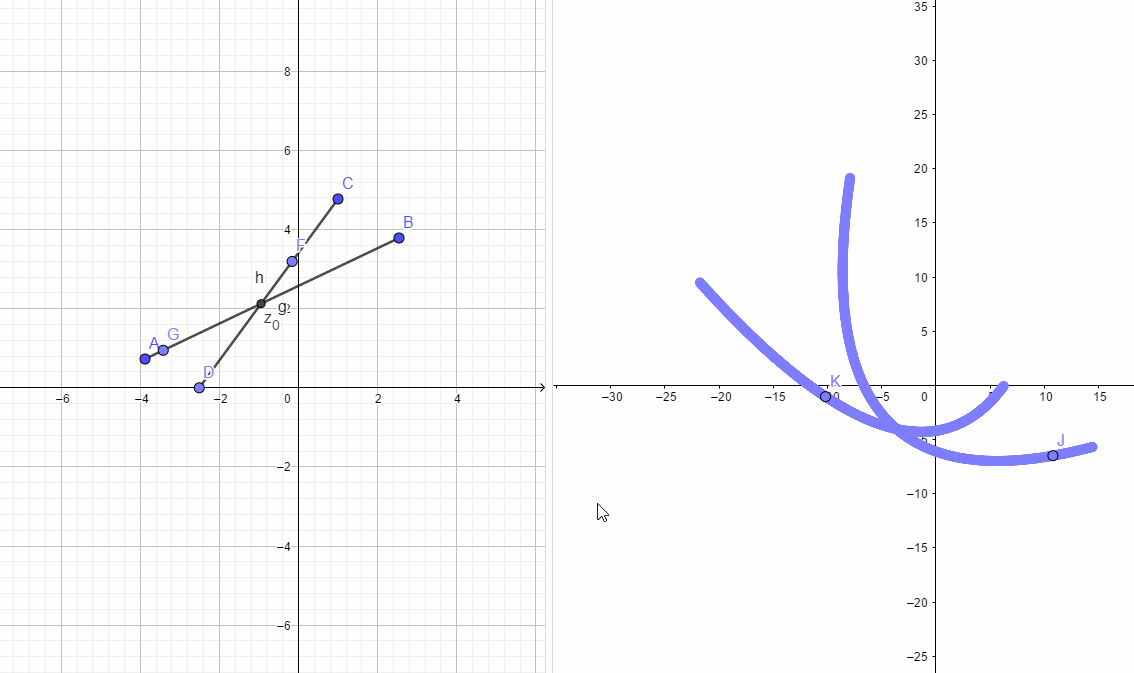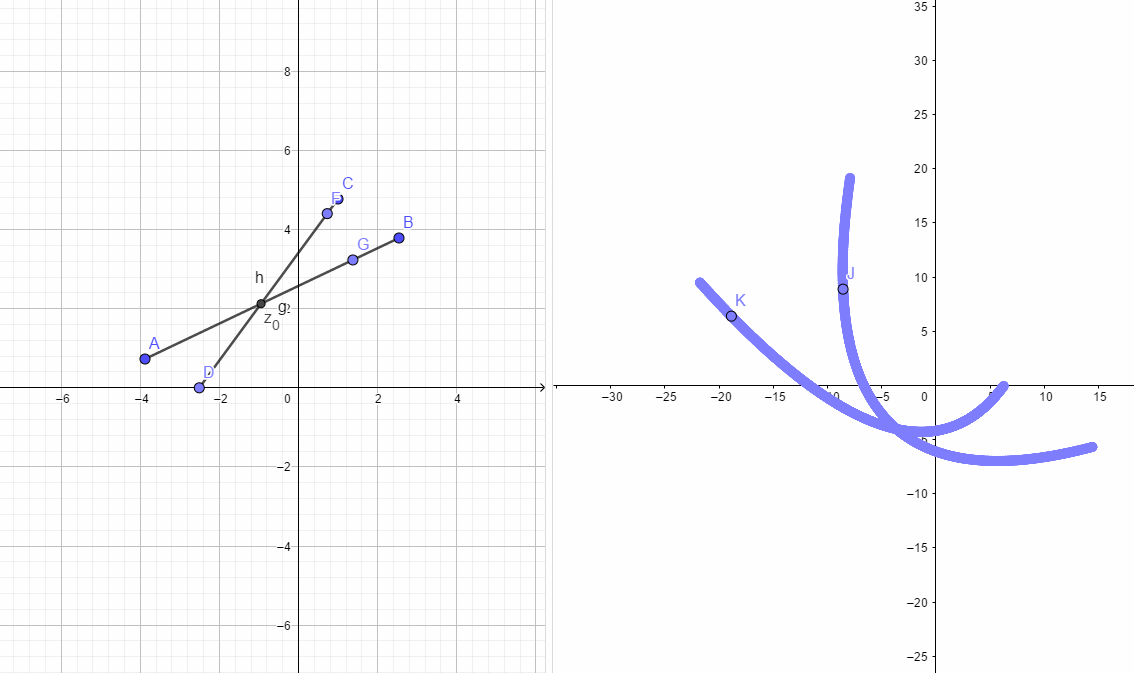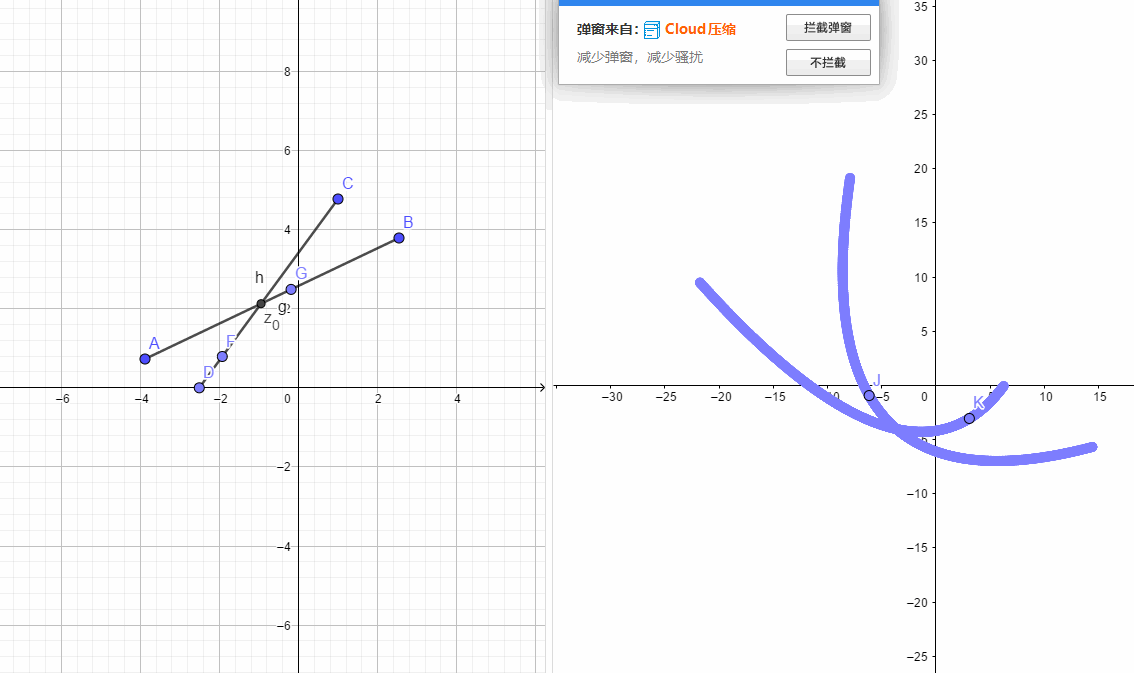
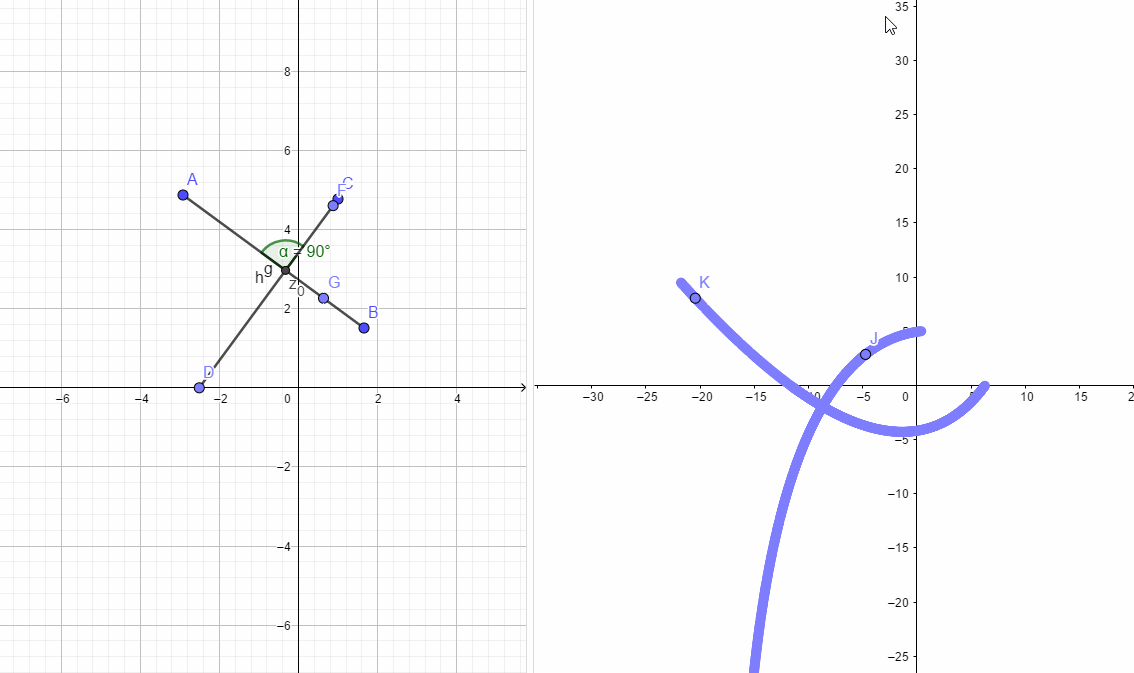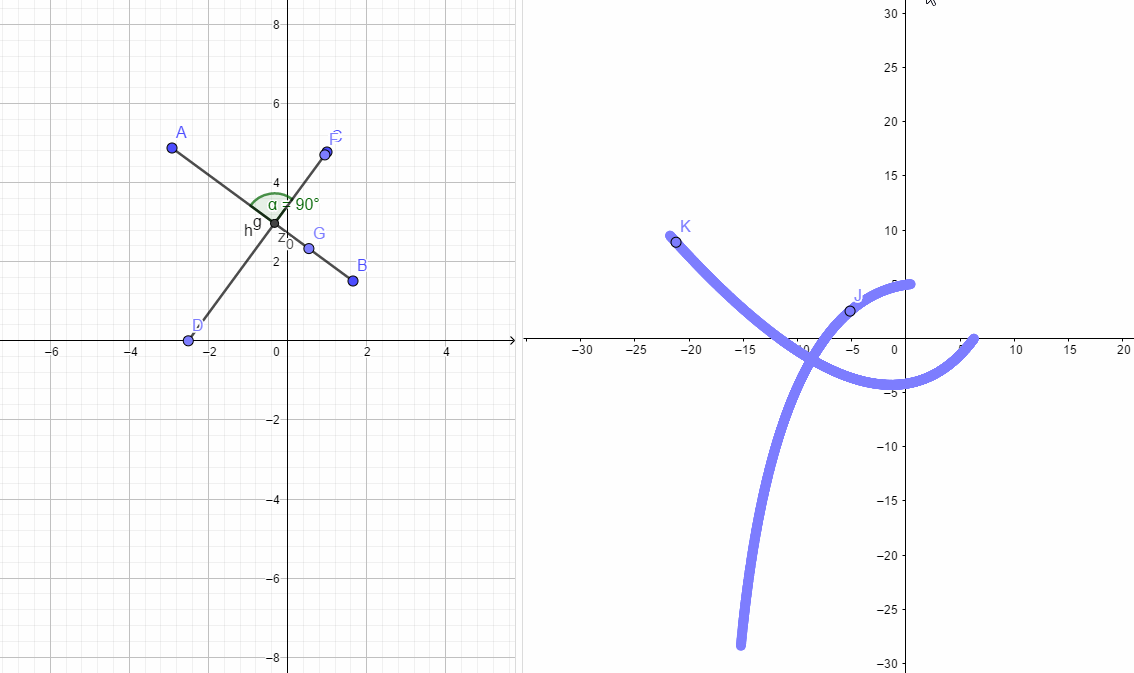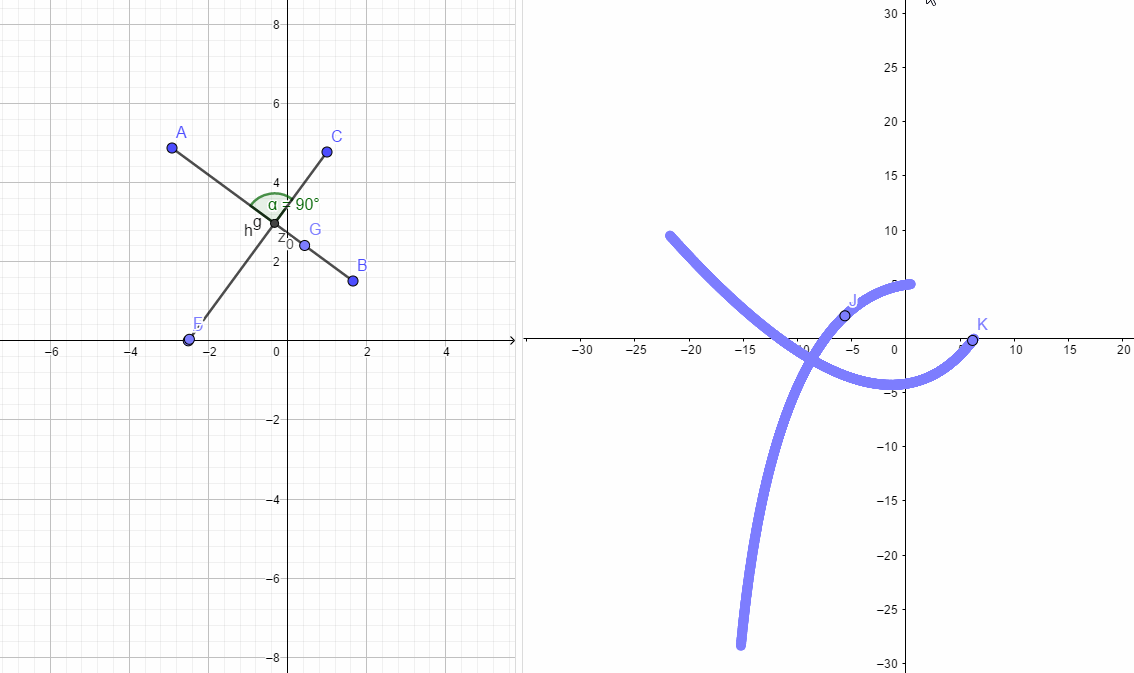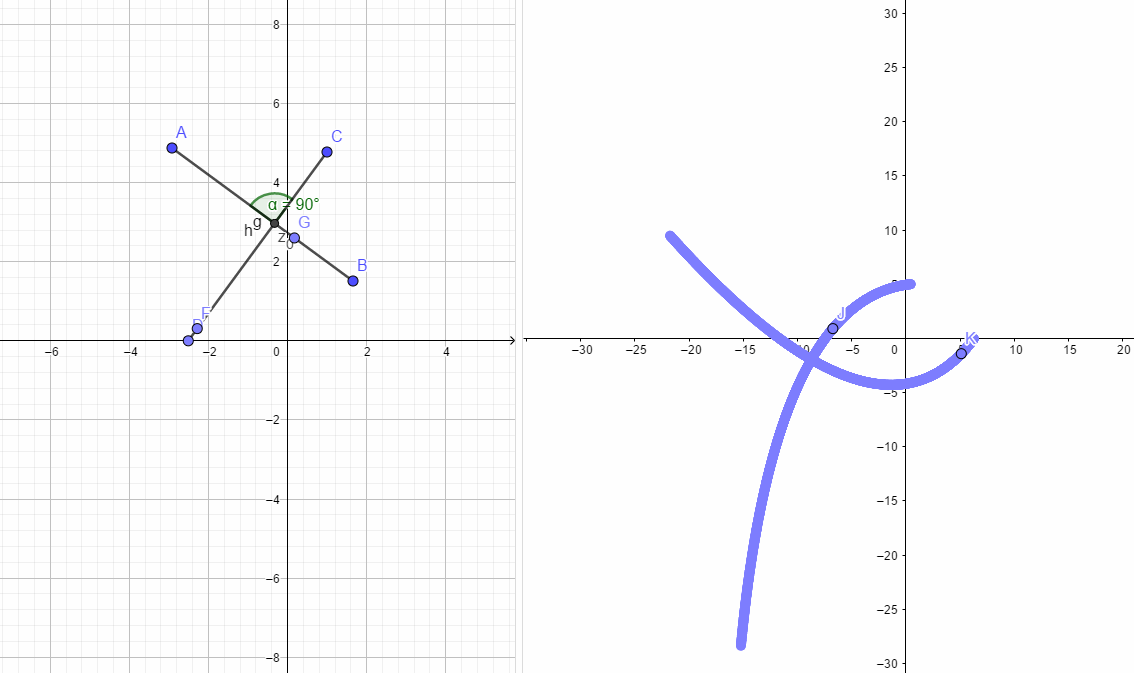
复变函数记
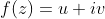
,其中
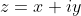
,所以可以得到
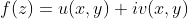
,其中x, y是实数,u,v是他们的实函数,如果
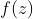
解析,那么
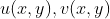
有什么关系呢?取
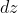
为两个特殊的方向,分别平行于实轴和虚轴接近
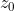
点。
对于AB方向,趋近方式为
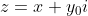
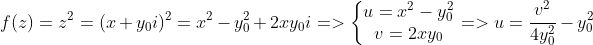
为开口向右的抛物线
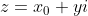
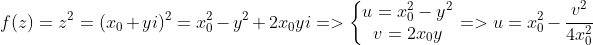
为一副开口向左的抛物线.
由于只含有固定值的平方项,所以关于非固定的对称轴对称的两条直线映射到同一条抛物线.
关于保持直角的映射,可以通过下面的代数证明看出来
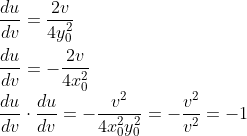
斜率正交,保持直角的性质得到证明.
如下图所示:
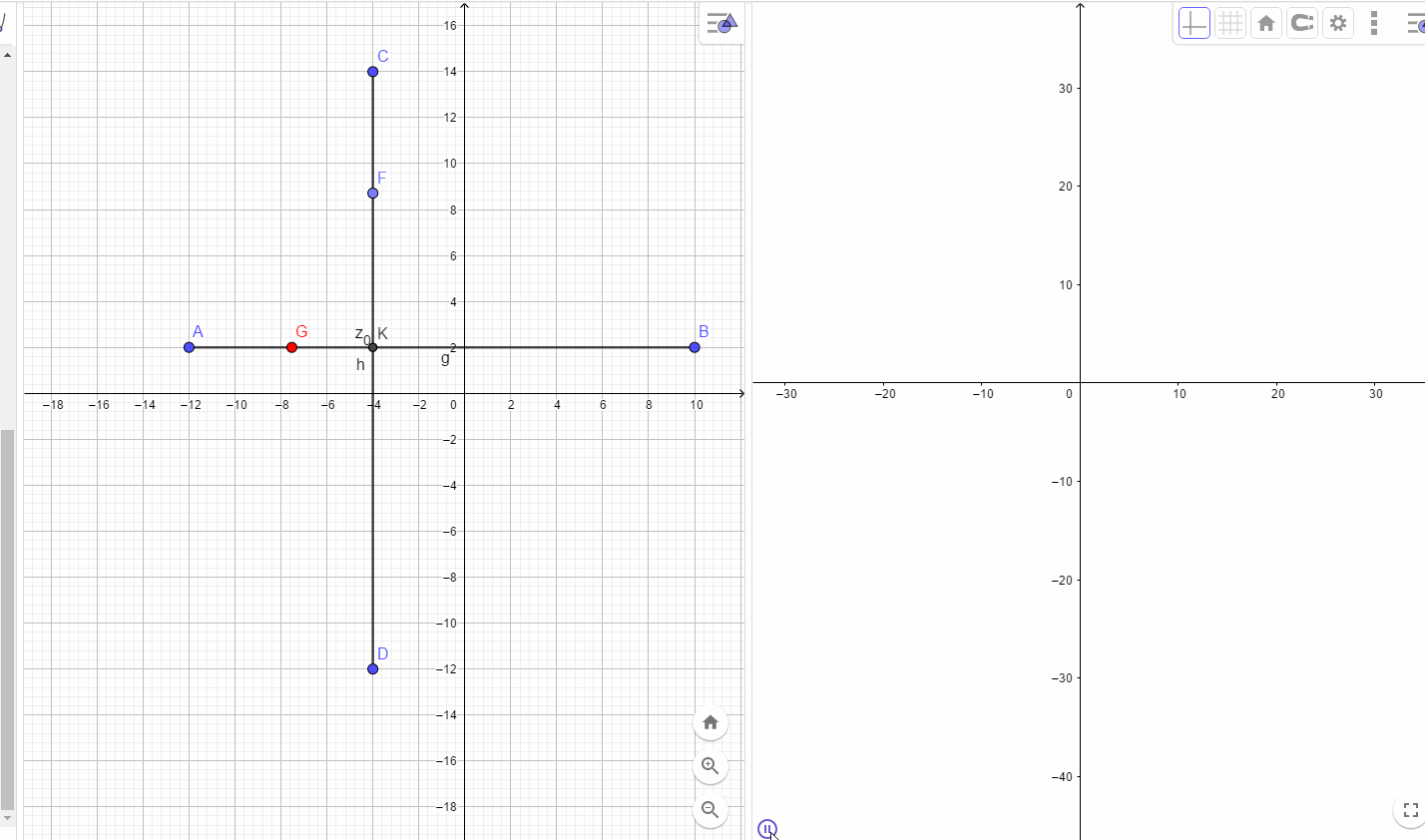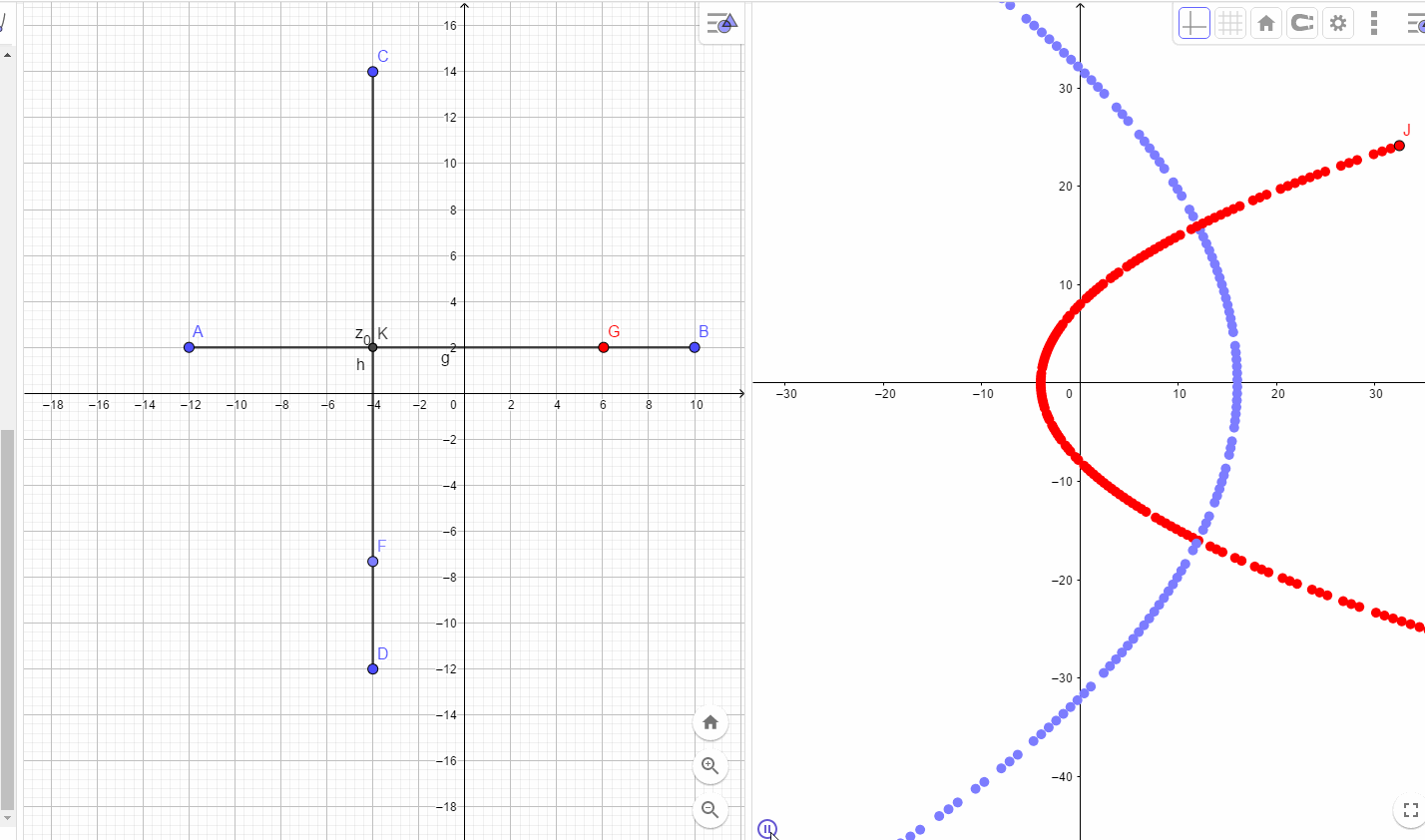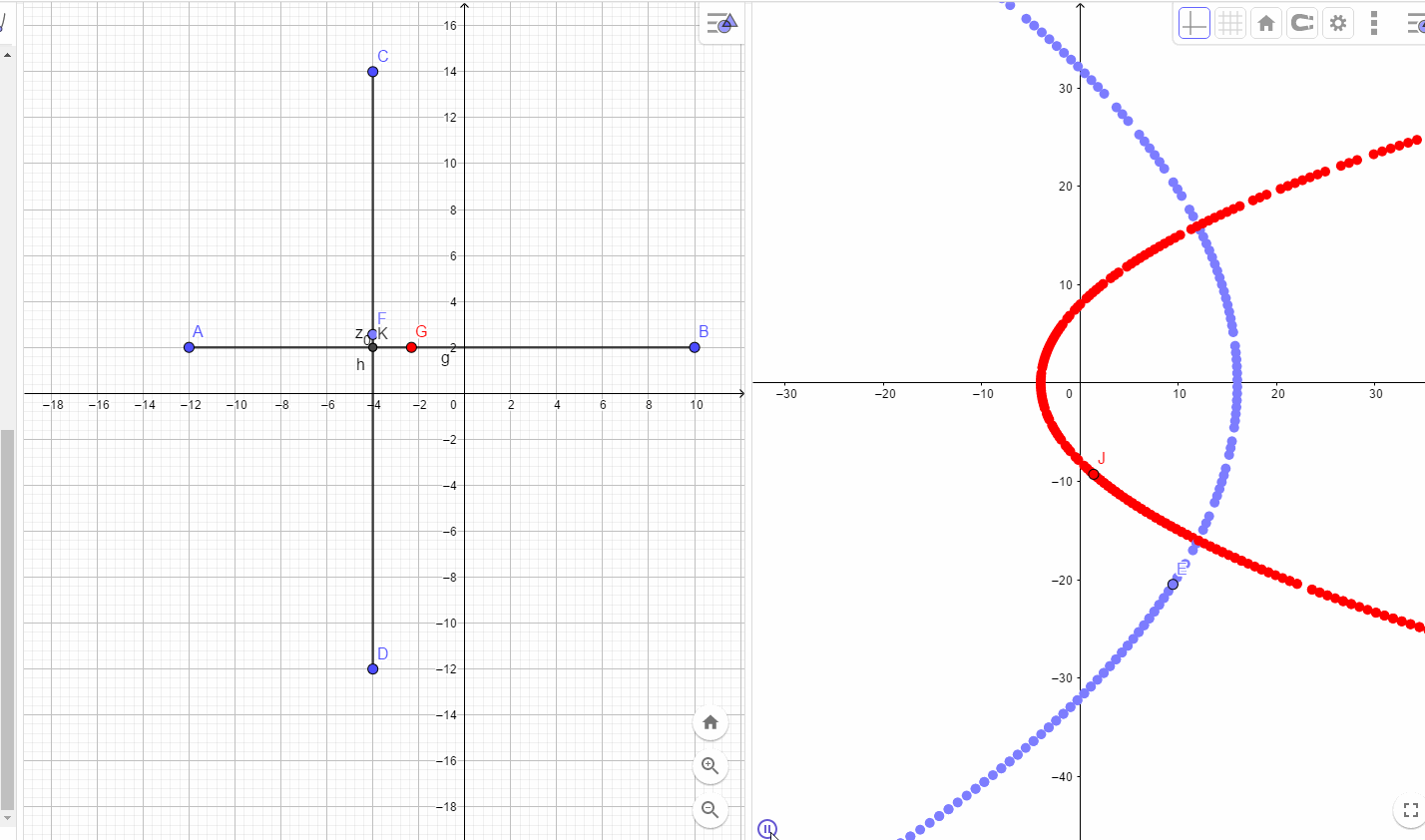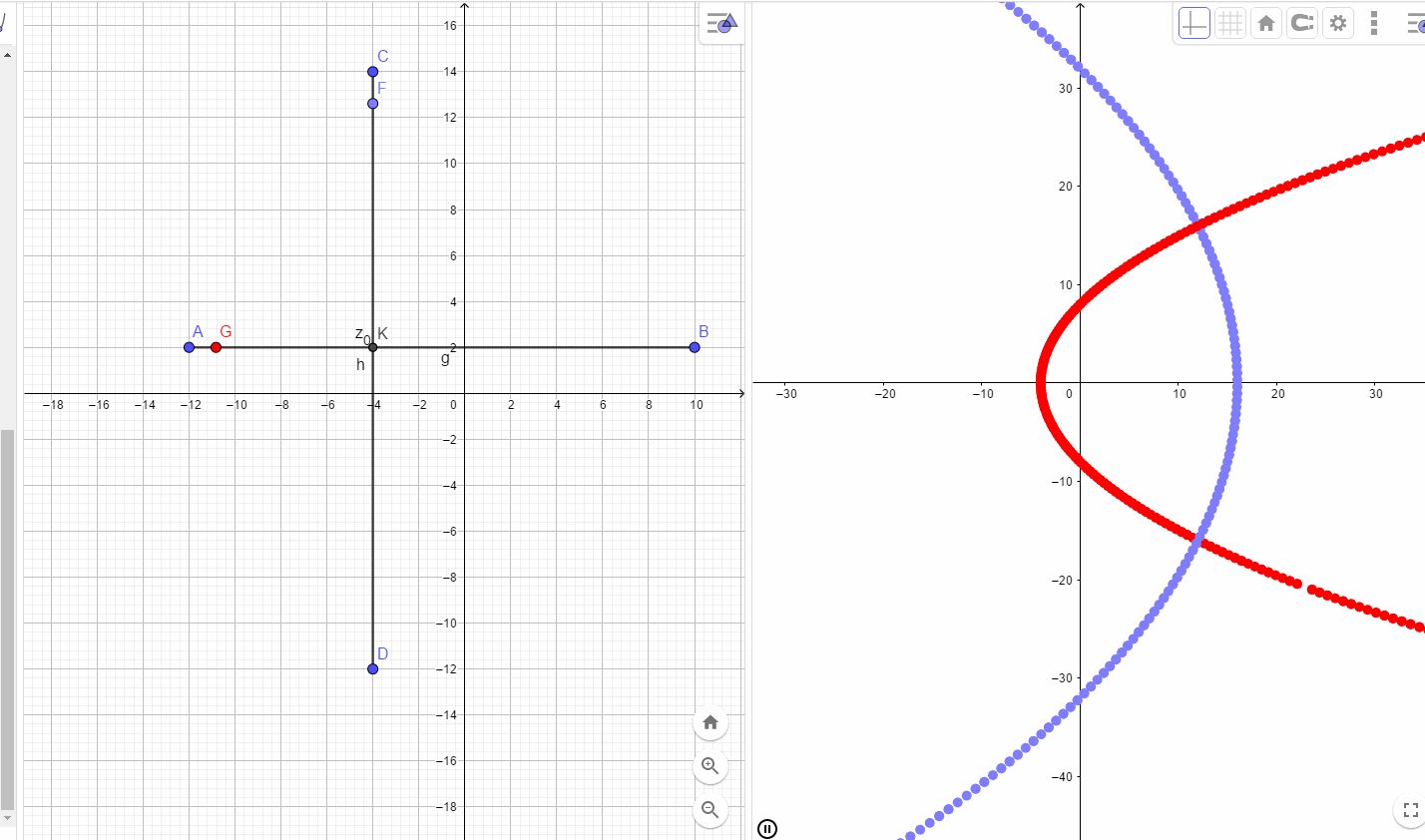
分析交点时刻的情况,根据可微的条件,下图的两个三角形应该全等,所以,同样可以得到C-R方程:
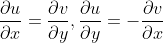

与线性空间变换的关系:
上面通过几何和代数证明,柯西-黎曼方程的几何意义,就是在变换(这里是复变函数求导)前后,保证一个稳定的伸缩率和转动角的变换.
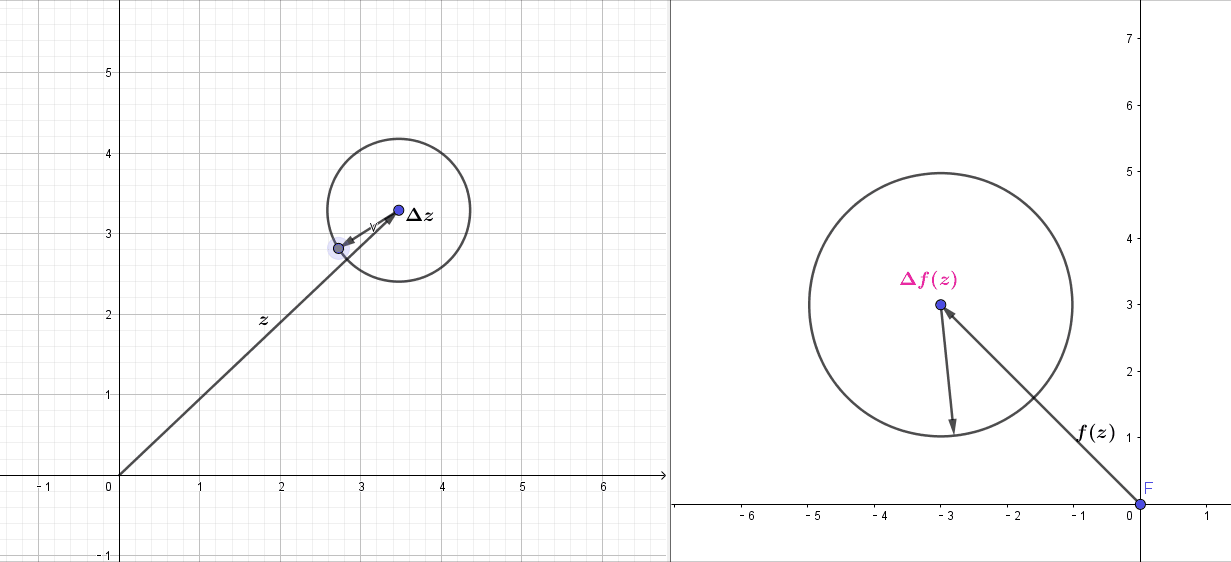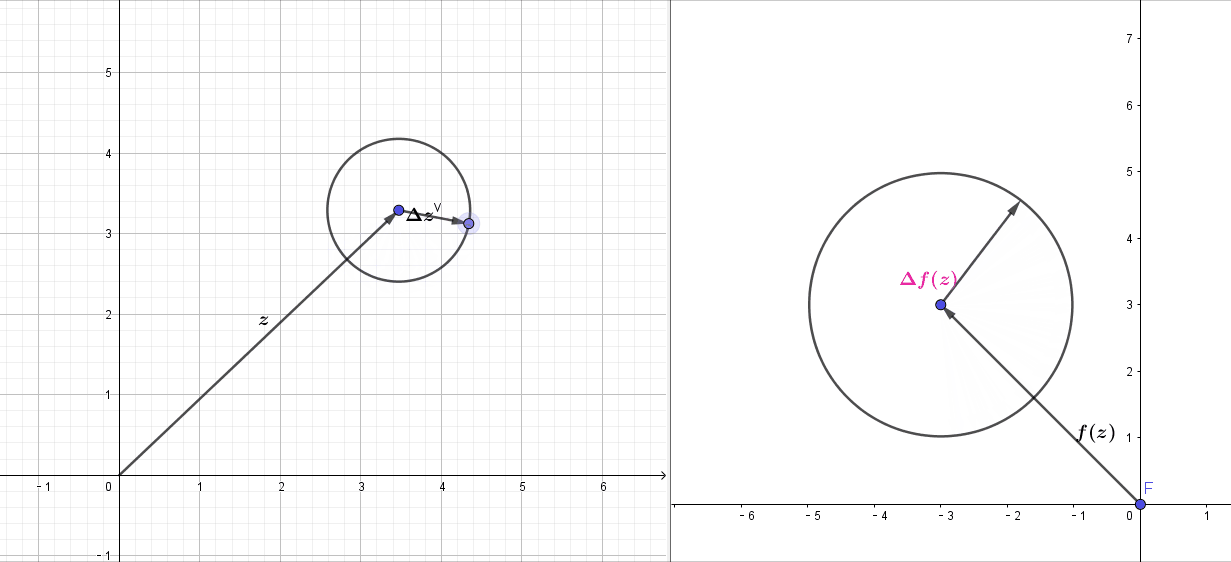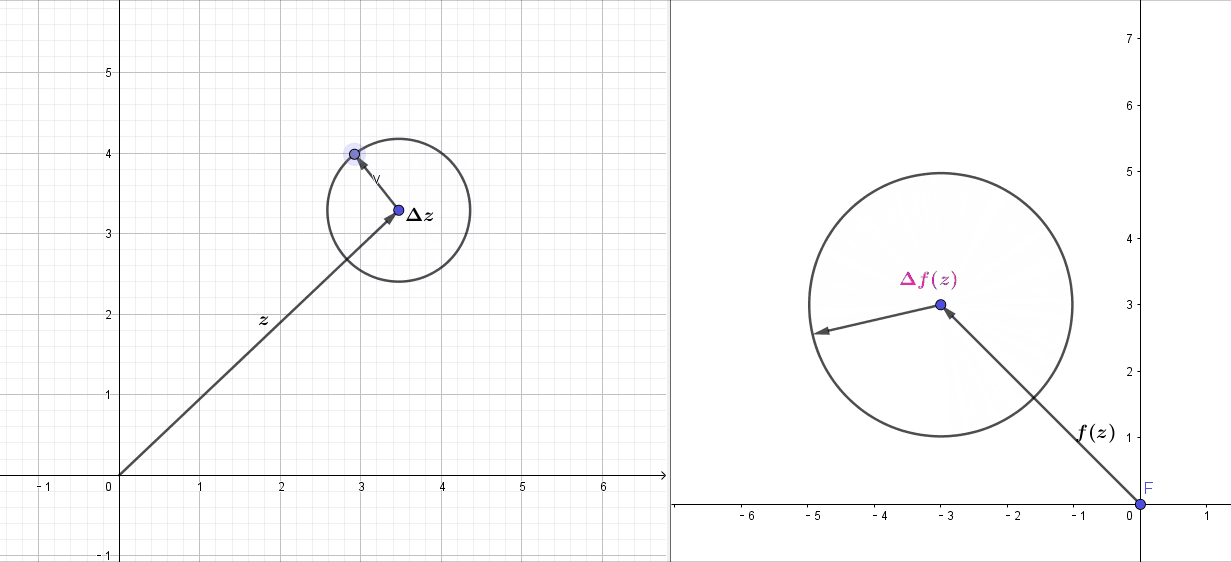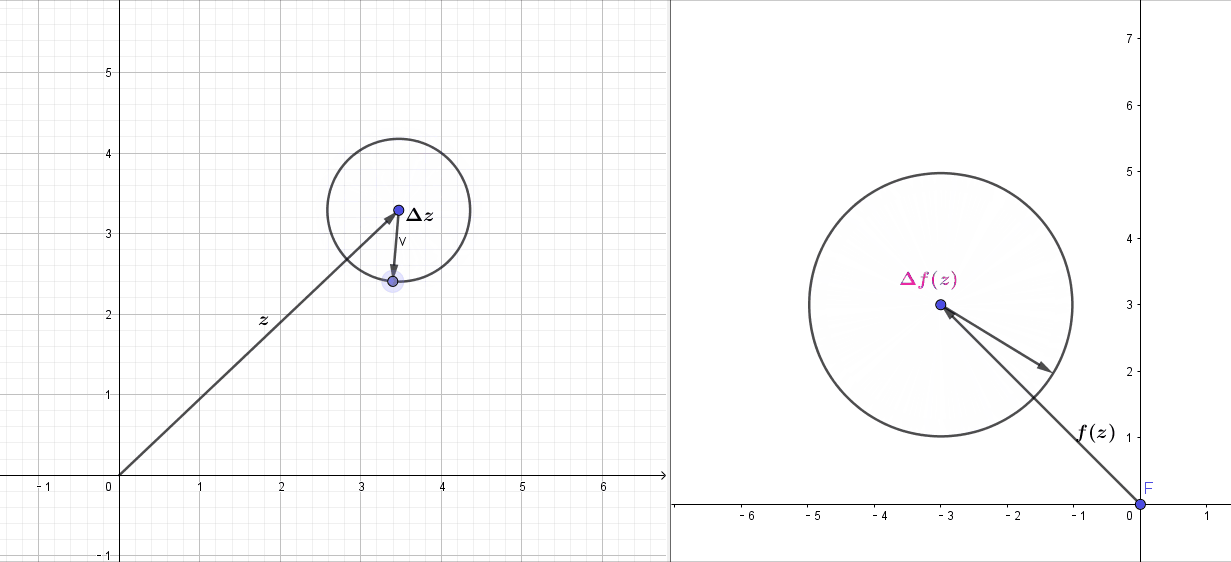
满足柯西-黎曼方程的可微复变函数,局部的变换效果就是那些可以转换为伸(拉伸)扭(旋转固定的角度
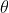
)的映射,即再点的某个区域内,从这一点出发的无穷小复数摄动下,变换后满足同样的俯角变换和幅值变换,微观上,就是可以将一个微小的圆变换为微小的圆,如上图,局部的微小圆变换左边的
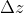
经过变换后,
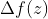
仍然是一个圆,这样
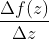
才能保持不变.
关于线性空间变换的种类,线性代数和线性空间理论中介绍是最多的,所以,复变函数可微的两个条件,
1.相同的伸缩因子
2.相同的转动角
可以对应到线性空间理论中的变换矩阵,首先是伸缩因子
1.伸缩变换用

表示2.转动变换最好理解了,对于逆时针方向旋转
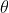
的变换,可以用矩阵
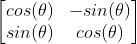
表示
两个变换的复合,就是
而可以看到,用
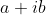
乘以
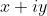
也将会得到一个变换:
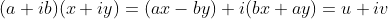
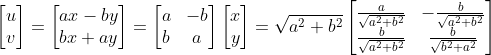
可以看到,这两变换何其相似,也就是说,复变函数可微性,对应了线性空间中的一类变换.



















