复变函数可视化以及代数基本定理

复变函数:

我们生活的世界是三维的，需要三个坐标信息才能清晰描述一个物体的位置，所以，人类很容易就能够理解三维以下的物体形状，二维笛卡尔坐标系和三维立体坐标系就是用来分析此类问题的数学工具。

但对于复变函数，情况有所不同。

以下面的复函数为例

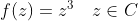
就无法像实变函数那样，在二维或者三维笛卡尔坐标系下绘制其图像。因为想要绘制出一对复数

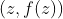
,需要４个维数,两个用来画

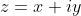
，两个用来画

.

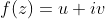
将函数展开，令

,

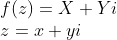
则可以得到:

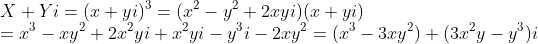
所以:

 

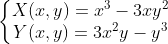
所以很明显，一元复变函数可以分解成两个二元函数，所以，无论在二维还是三维笛卡尔坐标系中，都无法表示四元

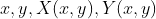
坐标的位置。

二维复空间可以解释做实的，但是四维的空间. 空间维度本来就不够用，笛卡尔坐标系用两个实轴来表示，委实有点浪费，实际上一维的实数空间用一个轴就够了。

在matlab中，是通过分解函数的实部和虚部来实现的，实部用三维笛卡尔坐标系的z轴表示，虚部用颜色表示，xOy表示整个复平面，绘制出来是这个样子:

颜色分析并不直观，有没有办法可以将虚轴的值也通过坐标截距表示出来呢？

问题转化为，如果用三维空间笛卡尔坐标系标识四维函数的问题，方法有两个:

1.用两个笛卡尔坐标系，　分别绘制

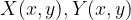
2.在一个笛卡尔坐标系内，分开绘制

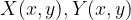
这有点像变成领域的，空间时间互换问题，二者不可兼得，这也是大自然的普遍规律。

下面采用第二种，用geogebra 将

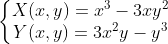
分别绘制在一个笛卡尔坐标系内:

图有些乱，但大体上能够看出绿色和品红色的是两个不同函数的图形，绿色是X(x,y),品红色是Y(x,y)左边是整个立体图形在XOY平面上的投影，立体上，两个图形完全一样，只是旋转了角度。

XOY平面上一条条的是图形的等高线，也是图像上具有相同实部和虚部的点在XOY平面上的投影，每个投影有三条分支，围绕中心原点在圆上呈现对称分布，由于两个图形完全相似，所以ＸＯＹ平面有两组一共六条投影线，

每两条分别来自不同函数的等高线的交点在复平面上的坐标表示方程

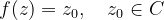
的一个解，也就是图中等边三角形的三个顶点，所以可以看到，对于任何

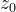
，方程均有三个解，围绕圆周均匀分布。当

的时候，也就是

得出的方程是每个图像的各三条渐近线.

模曲面:

从几何的角度看问题，在每个复数点

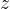
上安置立坐标垂线，它的长度等于多项式f(z)在这一点的模，这些立坐标的端点形成某一曲面Ｍ，我们把它叫做多项式f(z)的模曲面，这样就可以将复变函数的实部和虚部一起考虑，而不用分别

绘制实和虚部，模曲面实际上将实部和虚部作为一个整体来看，这样就减少了一个维度，四位塌缩成了三维，就可以画在三维坐标系上了。

模曲面有一些性质:

1.在全部复平面内，模曲面不会下降到复平面以下，模不可能是负的。

2.对于复平面上任何一点z,这个曲面上有一点，并且仅有一点位于这个点的上面或者就是这个点本身，说明与复平面接触。

3.当z在复平面上连续运动时，这个曲面的点的立坐标

连续变动。4.由于多项式的根要么是实根，要么是共轭复根，因为假如复数

是多项式的一个根，那么：  

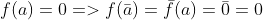
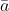
也是一个根，所以M曲面一定关于实轴对称.

设

对于一次函数

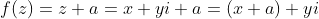
模曲面与复平面有一个触点，并且固定在x轴上，坐标为

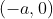
对于二次复变函数:

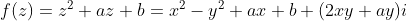
与复平面的触点有两个，要么是共轭复根，要么是两个实根，这也符合二次函数根的分布情况。

下面绘制

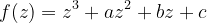
的模曲面：

则:

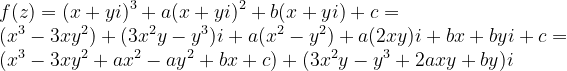
所以

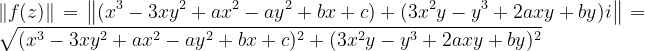
图形为：

三个实根的情况：

octave求得算数解:

对于四次的情况：

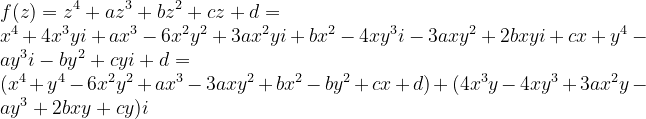
其对应的模曲面形状如下所示，有四个点和复平面接触，为其零点。

图中可见，方程的次数和根的个数似乎有某种对应关系，事实上，次数等于根树，这是代数基本定理，模曲面方程和复平面的n个接触点为零点，就好像有n根支柱将整个曲面支撑起来，不断变化a,b,c,d的值，这三个支柱相对位置在复平面上会发生变化，但始终和复平面有接触，根据达朗贝尔引理（了解就好，对理解关系不大)，曲面上的任何一个极小值点都是０，没有一个极小值是正的非零值。

这表示复平面上始终有三个点，使

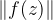
=0,由于复数等于零，与它的模等于零是同义的，

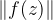
为０的充分必要条件是

等价于，多项式

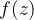
＝０

有三个根。

这是由代数基本定理决定的：代数基本定理是说，任何复系数一元n次多项式 方程在复数域上至少有一根(n≥1)，由此推出，n次复系数多项式方程在复数域内有且只有n个根（重根按重数计算）。代数基本定理在代数乃至整个数学中起着基础作用。 据说，关于代数学基本定理的证明，现有200多种证法。

 代数基本定理强调的有一个根，而不是n个根，之所以这样，是因为多根可以由１个根推导出来,设:

设

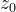
是f(z)的一个根，用

去除以

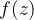
,由于除式是１次的，因此余数就是一个常数

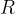
(根据多项式整除规则，如果遗留带z的多项式做余数，则整除规则可以继续下去，直到只剩下常数项),所以:

式中

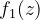
是一个n-1次的多项式，而Ｒ是常数，用

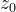
代入：

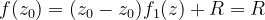
由于

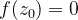
所以

R=0

即

同理，如果代数基本定理正确的话，必定

..............

所以，如果存在１个根，就一定存在n个根，代数基本定理只需要说明１根的情况即可。

这n个根之间没有要沿实轴在整个复平面上呈现对称分布，除此之外，没有其它形状要求（比如是否一定要共圆？下图五个根在实部为-2的复直线上，显然不可能共圆).

尝试以几何的方式去理解：

对于形如：

　为复数

将形式改写为:

 

    

明确几点：

1.

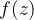
是从复数域到复数域的一个映射. 2.当

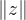
增大时，

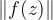
无限接近

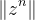
,这是由于

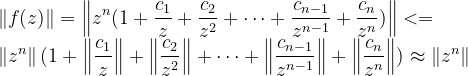
  接下来，设复平面上一圆

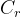
,圆心在原点，半径r足够大。由于r足够大，当z在

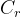
上运动时，

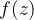
主要由其高次项决定，也会非常接近  

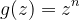
当z围绕

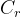
旋转一圈时，根据复数乘法法则

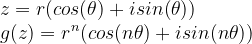
当

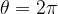
时候，

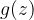
的幅角运动

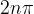
，也就是旋转n 圈。由于r足够大时，

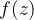
和

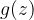
足够接近，所以也旋转n 圈。

然后，想象一下

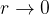
当z的辐径逐渐收缩到复平面原点的时候，

由于r足够大的时候，原点和

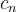
都包含在

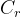
内部（总是可控的，只要r足够大，一定满足这个条件) ，那么

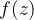
在收缩过程中，必定扫过原点，也就是说存在最少一次的

得证。

结合Ｍ曲面图，

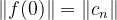
而

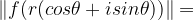
足够大

并且上面已经证明了会经过原点。

所以，在收缩过程中，M曲面必定有点与复平面“摩擦"接触！

联想到自动控制原理中介绍跟轨迹问题，也可以用Ｍ曲面理论去理解．

例如：

对于开环传递函数为

　　

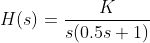
的控制系统,如下图所示：

其闭环传递函数为：

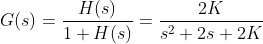
所以特征方程

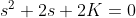
的根是:

　　

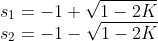
如果想知道随着开环增益Ｋ变化，控制系统的稳定性如何变化，可以绘制特方程的Ｍ曲面:

另

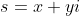
则

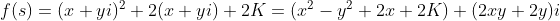
所以，Ｍ曲面方程为:

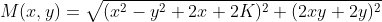
Ｋ＝0,其图像是两个不同的实根:

K=0.5,两个相同的实根

Ｋ>0.5的时候，是两个分离的复数根．

所以，复平面上的跟轨迹实际上是：

kaihuanfenzi=[0,2];
kaihuanfenmu=[1,2,0];
sys=tf(kaihuanfenzi,kaihuanfenmu);
rlocus(sys);
axis([-8 2 -2 2]);

所以控制系统的稳定性问题实际上是多项式在复平面上的根分布问题．

数形结合能够反映代数和几何之间的深层联系,geogebra是数形结合分析问题的利器。

结束！